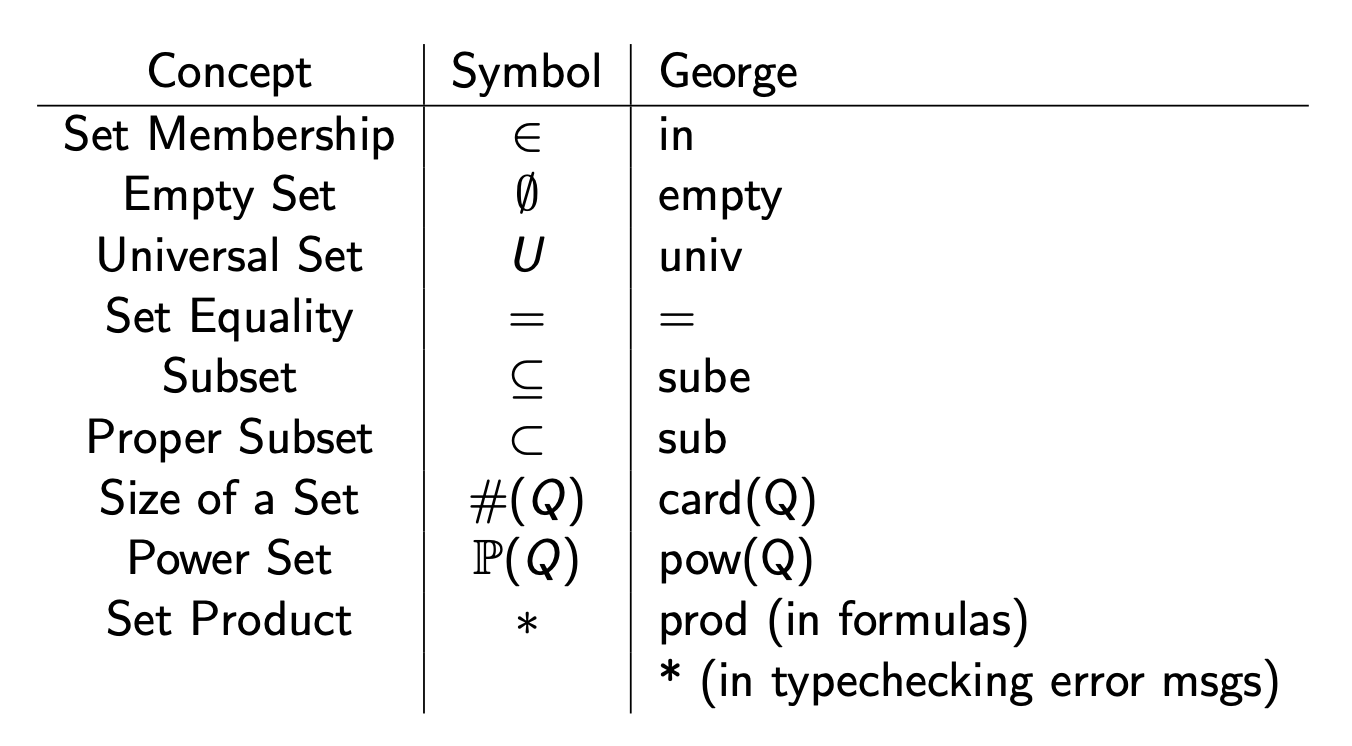
Binary Relation

In mathematics, a binary relation associates elements of one set, called the domain, with elements of another set, called the codomain.

I am surprised they never taught us this. NOTE: Finally learning this in SE212

Relations are sets. A relation, $R$, is a subset of the Cartesian product of two (or more) sets.

• $R\subseteq C\ast B$ also $R\in \mathbb{P}(C\ast B)$

We can state that R is a relation from a set C to a set B as a type:

• $R:C\leftrightarrow B$ or $R:\mathbb{P}(C\ast B)$

IMPORTANT: Note that the symbol $\leftrightarrow$ above does not mean transformational proof in this context.

A binary relation is a set of pairs. We can also have a ternary relation, which would have a set of 3 elements.

Relation

Wow, SE212 exposed me to this new way of thinking about Functions as mappings between sets to sets (well yea, but notation is different). This is for relation

For relation $R:A\leftrightarrow B$

Domain $dom(R)=\{x:A\mid \exists y:B\cdot (x,y)\in R\}$ Range $ran(R)=\{y:B\mid \exists x:A\cdot (x,y)\in R\}$ $dom(R)$ and $ran(R)$ are both sets. $A$ and $B$ are universal sets.

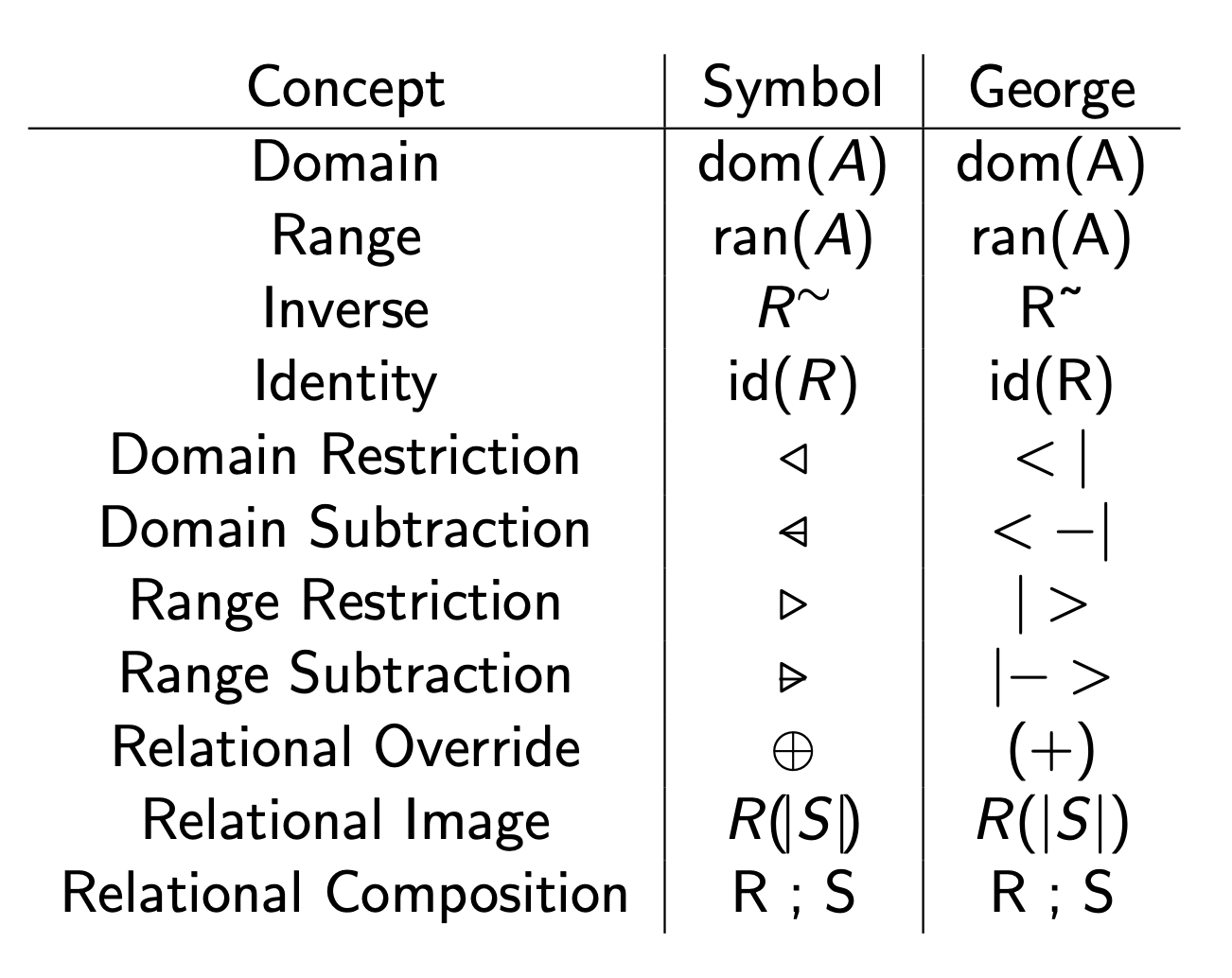
Inverse Relation For a binary relation, $R$, its inverse relation, $R^{\sim }$, is the relation created by reversing the order of the elements of the pairs of $R$.

For $R:A\leftrightarrow B$, Axiom [Inverse] $R^{\sim }=\{(b,a)\mid (a,b)\in R\}$ We have the following properties for inverse relations:

• $(R^{\sim }{)}^{\sim }=R$
• $dom(R^{\sim })=ran(R)$
• $ran(R^{\sim })=dom(R)$

Identity Relation The identity relation for a set $B$, written as $id(B)$, is the pairing of every element of $B$ with itself. $id(B)=\{(a,a)\mid a\in B\}$ I don’t know why this is useful, but oh well, we’ll see.

Relational Composition For three sets $A$, $B$ and $C$, and two relations on them $R:A\leftrightarrow B$, and $S:B\leftrightarrow C$, the relational composition of $R$ and $S$ is the relation containing the pairs $(a,c)$, such that there is an $b\in B$, and $(a,b)\in R$ and $(b,c)\in S$. It is pronounced “$R$ followed by $S$”.

$R;S=\{(a,c)•a:A,c:C\mid \exists b•(a,b)\in R\wedge (b,c)\in S\}$

Relational Image This is sounding way too complicated for no reason. $S$ is a set, and $R$ is a relation. $R(|S|)$ gives the image of $R$ restricted to $S$ as a set.

If you do $R▷S$, that would still give you a set of pairs, but you want a set of the image/range generated.

$R(|S|)=\{y\mid \exists x•(x,y)\in R\wedge x\in S\}$

Restrictions

The trick is to remember that

• domain = (put set on) left to restrict the intake of relation $R$
• Range = (put set on) right to restrict output of relation $R$

Domain Restriction retains only the pairs whose first elements are part of a set $S◁R=\{(a,b)•a:A,b:B\mid (a,b)\in R\wedge a\in S\}$ Domain Subtraction retains the pairs of binary relation $R$ whose first elements are NOT part of set $S$ The symbol is different but I can’t get it to show up on Obsidian. It has an extra slash $S◁R=\{(a,b)•a:A,b:B\mid (a,b)\in R\wedge \neg (a\in S)\}$

Range Restriction retains only the pairs of relation $R$ whose second elements are part of set $S$ $R▷S=\{(a,b)•a:A,b:B\mid (a,b)\in R\wedge b\in S\}$

Range Subtraction retains the pairs of relation $R$ whose second elements are NOT part of set $S$ $R▷S=(a,b)•a:A,b:B|(a,b)\in R\wedge \neg (b\in S)$

Using relational overriding, we can “update” a relation $R$ with another relation $S$ where the pairs of $S$ are added to the relation, and pairs in $R$ with the first element of pairs in $S$ are eliminated (think of it like being overwritten)

$S$ is NOT a set here.

$R\oplus S=(dom(S)!◁R)\cup S$ R ⊕ S = ((dom(S) !◁ R) ∪ S = \set{(a, b) | (a, b) ∈ R ∧ a ̸∈ dom(S) ∨ (a, b) ∈ S} This is NOT the same as relational composition.

Functions

This is a new way to think about functions as a relation.

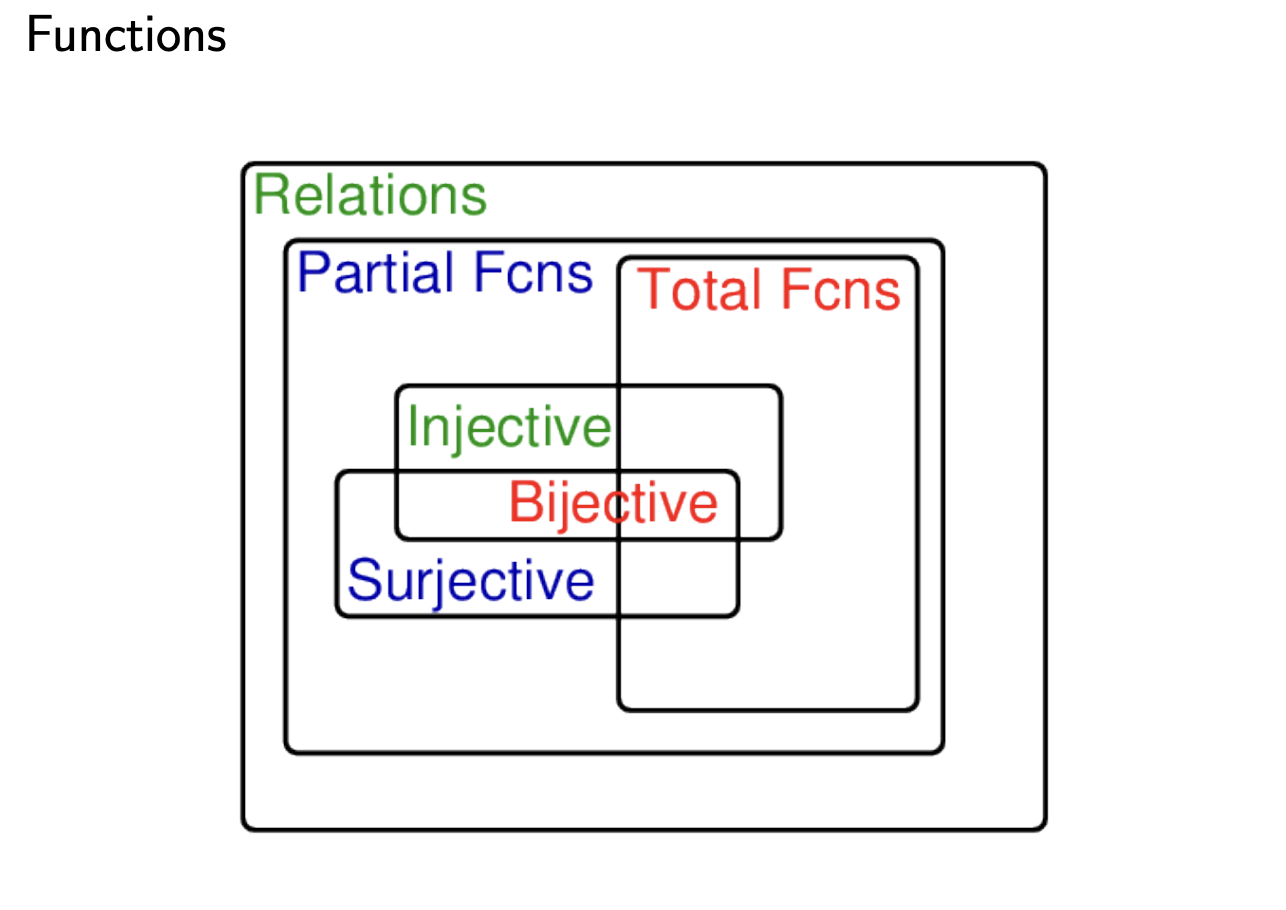
A Function is a Relation in which each domain element is associated with a unique range element.

A relation $f:A\leftrightarrow B$ (equivalently $f\in \mathbb{P}(A\ast B))$ or $f\subseteq A\ast B$) is a function if and only if $\forall x:A•\forall y,z:B•(x,y)\in f\wedge (x,z)\in f\Rightarrow y=z$

• Functions can be classified as total, surjective, injective, and bijective.
• Functions are also called mappings.
• $f(x)$ is called the application of $f$ to $x$.
• $f(x)=y$ is the same as $(x,y)\in f$ if $f$ is a TOTAL function.

Partial Function

For a function f from set A to set B, the domain of $f$ may include all, some or none of the elements of A. If an element of A is not in the domain of the function we say that it is “undefined” for that element.

Partial functions are the most general kind of function. All functions are partial functions.

The set of partial functions from A to B is: $\{f:A\leftrightarrow B\mid \forall x:A•\forall y,z:B•(x,y)\in f\wedge (x,z)\in f\Rightarrow y=z\}$

This is exactly what we said was necessary for something to be a function.

Function Space

A set of functions is called a function space. The set of (non-total) functions (note this is from SE212, they use these really weird symbols that I can’t use in SE212, they use these really weird symbols that I can’t use in LateX):
$A7\to B=\{f:A\leftrightarrow B\mid \forall x:A•\forall y,z:B•(x,y)\in f\wedge (x,z)\in f\Rightarrow y=z\}$

We can use the function space as the type of the function. f : A 7→ B means f is a partial function from A to B

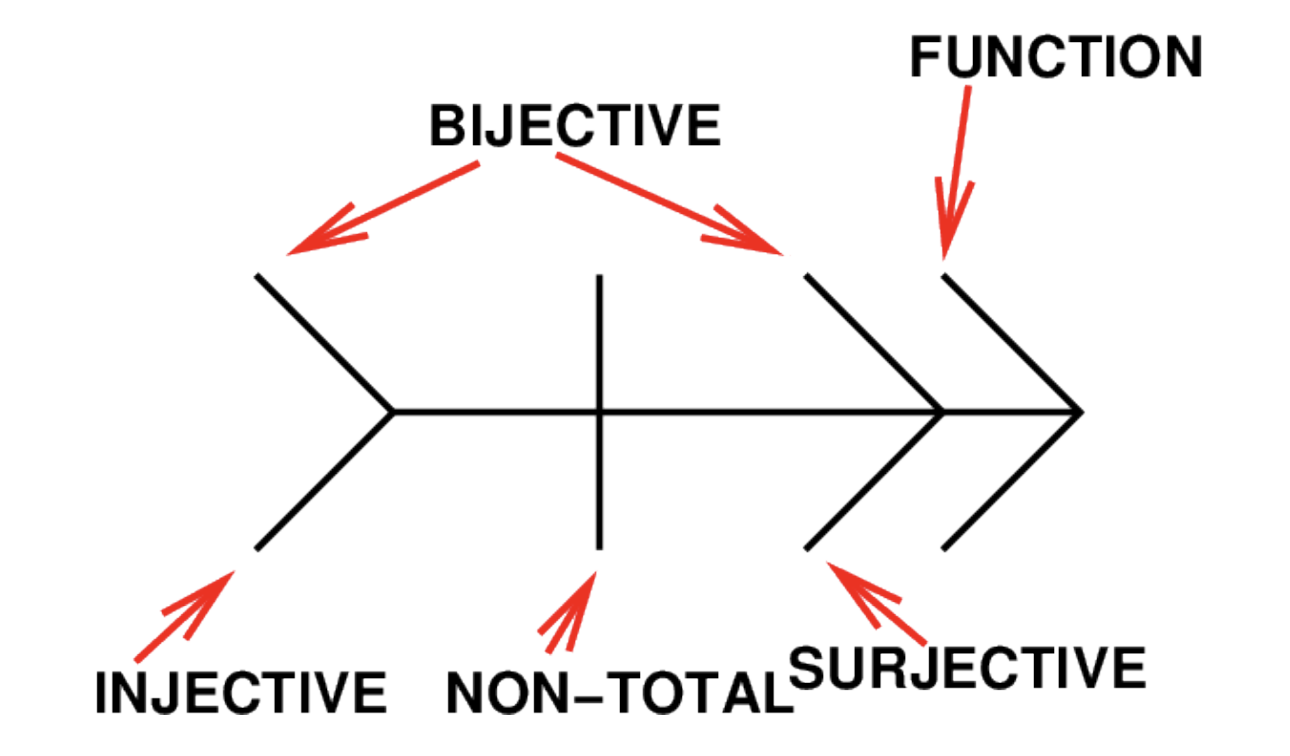Notation in SE212 for Injective, Surjective and Non-Total functions.

See Injective and Surjective Function for definitions.

Total Function

A total function simply means that it is defined for all of the domain.

A total function from set $A$ to set $B$ is defined for all the elements of $A$. Total functions are a subset of the set of partial functions from $A$ to $B$. $A\to B=\{f:A\mapsto B\mid dom(f)=A\}$ $f:A\to B$ means f is a total function from $A$ to $B$