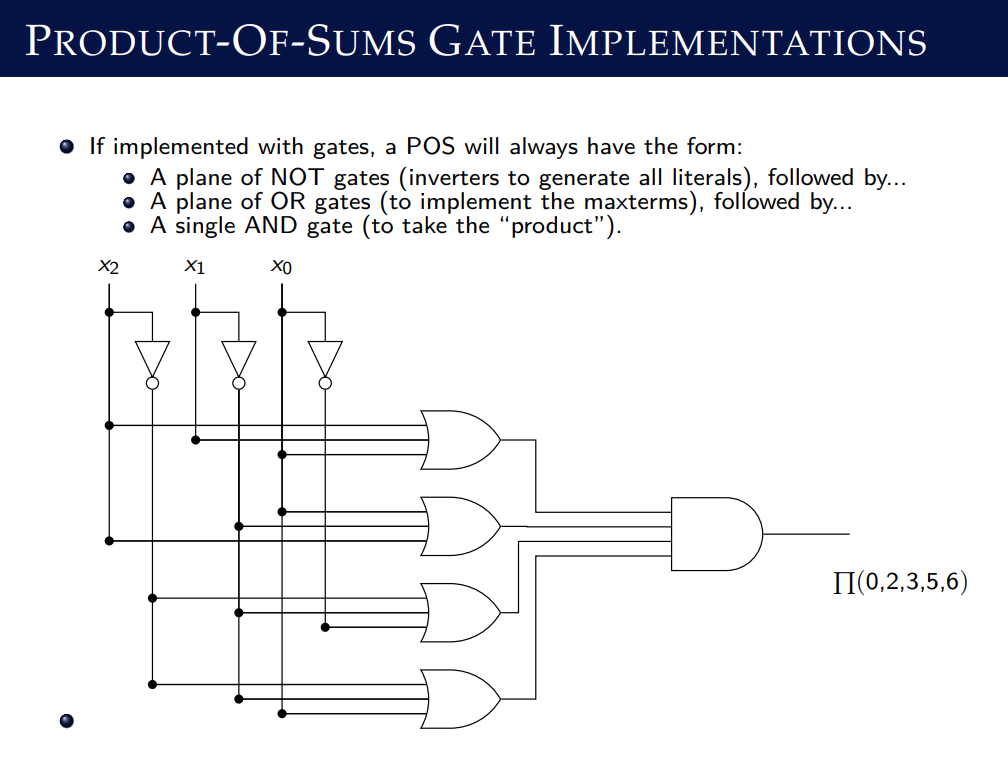
Product-of-Sums (POS) Form

A logic expression consisting of sum (OR) terms that are the factors of a logical product (AND) is said to be of the product-of-sums (POS) form.

Used when the output is 0. Sum of Products used when the output is 1.

Basically, look at the truth table and look at everywhere where the result is false (0). Then do the product of sums where those things are true.

POS Form and SOP Form are logically equivalent.

title: Standard POS
A **standard POS expression** is one in which all the variables in the domain appear in each sum term in the expression.
Ex: $(\overline{A} + B + C + D)(A + B + \overline{C} + D)(A + B + C + \overline{D})$ is a standard POS expression
 

Converting a Sum Term to Standard POS

Step 1. Add to each nonstandard product term a term made up of the product of the missing variable and its complement. This results in two sum terms. As you know, you can add 0 to anything without changing its value. Step 2. IMPORTANT: Apply rule 12 from Table 4-1: A + BC = (A + B)(A + C) Step 3. Repeat Step 1 until all resulting sum terms contain all variables in the domain in either complemented or noncomplemented form.

CIrcuit Implementation