Rolling Motion

Rolling is rotation about an axis that is translating.

Spinning, Skidding, Slipping

Spinning occurs when the rotational speed of the surface of an object is too high in comparison to the translational speed of the axis about which the object rotates. Ex: Truck in mud $v_{cm}<r\omega$

Skidding occurs when the translational speed of a rolling object is too high compared to the rotational speed of its surface. Ex: Drifting without wheels moving $v_{cm}>r\omega$

Slipping = spinning or skidding

Rolling Without Slipping

If an object neither spins nor skids as it rolls, its motion is called rolling without slipping (also called ideal rolling). $v_{translational}=v_{rotational}$ $v_{bottom}=0$ We have the following formulas, where $v_{cm}$ and $a_{cm}$ can be derived by taking the derivative.

$s_{cm}=r\theta$ We can say the above only because rotation speed is the same as translation speed. I am having a hard time wrapping my head around this. Visualize below, the CM is covering the same distance as the arc s. $v_{cm}=r\omega$ $a_{cm}=r\alpha$

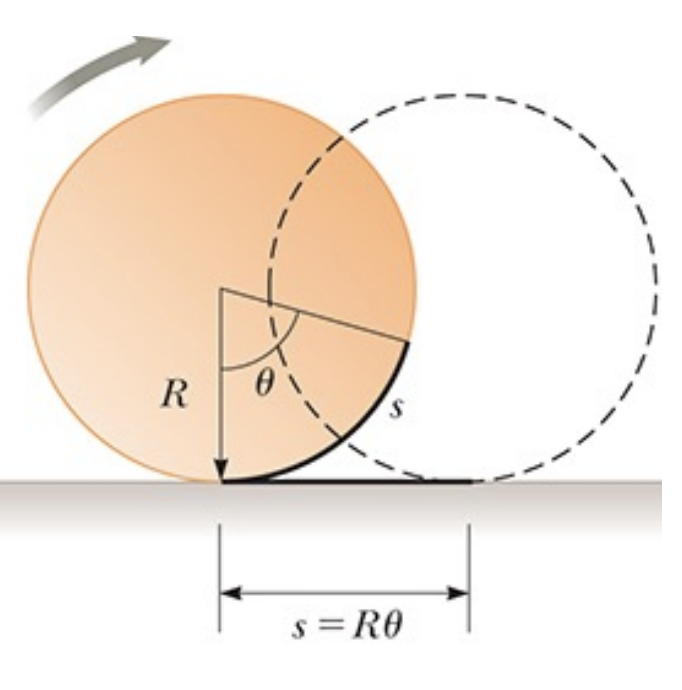
When we looked at Rotational Kinematics and Dynamics, we often thought of the problem of a fixed rotation axis. But now, consider that the rotation axis is moving.

For stationary, $v_{cm}=0$, so the formulas below still apply

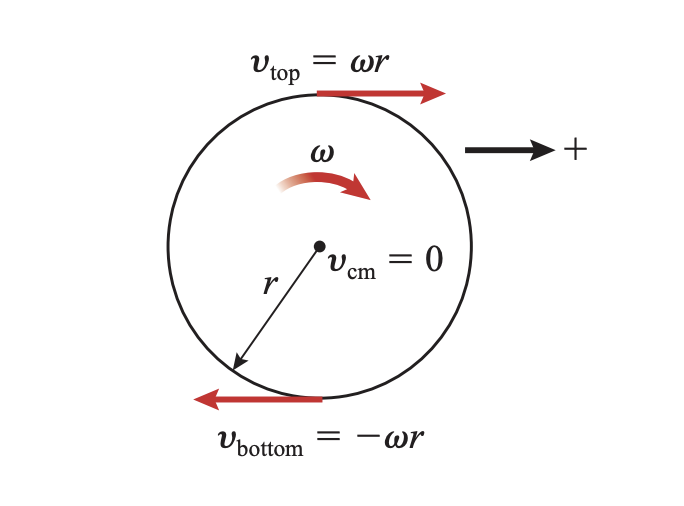$v_{top}=v_{cm}+\omega r$ $v_{bottom}=v_{cm}-\omega r$ $v_{top}=v_{bottom}+2\omega r$ Physics book, page 313.

Rolling as Rotation about the Moving Centre of Mass

Assuming no slipping, $v_{bottom}=0$ $v_{cm}=v_{bottom}+\omega r=\omega r$ $v_{top}=2\omega r$

Friction, Rolling horizontally vs on an inclined surface

Horizontal surface

• If pure rolling has not started, need at least one external torque to initiate rolling
• If pure rolling has started, friction no longer needed If an object is moving horizontally, there is no static friction.

Inclined surface

• Friction non-zero

Rolling Friction

Rolling friction can be quantitatively approximated using a coefficient of rolling friction. It results from deformation of object from surface.

Misc. Knowledge

When you add spin angular momentum, it stabilizes.

Billiard ball thing#to-review Rolling without friction