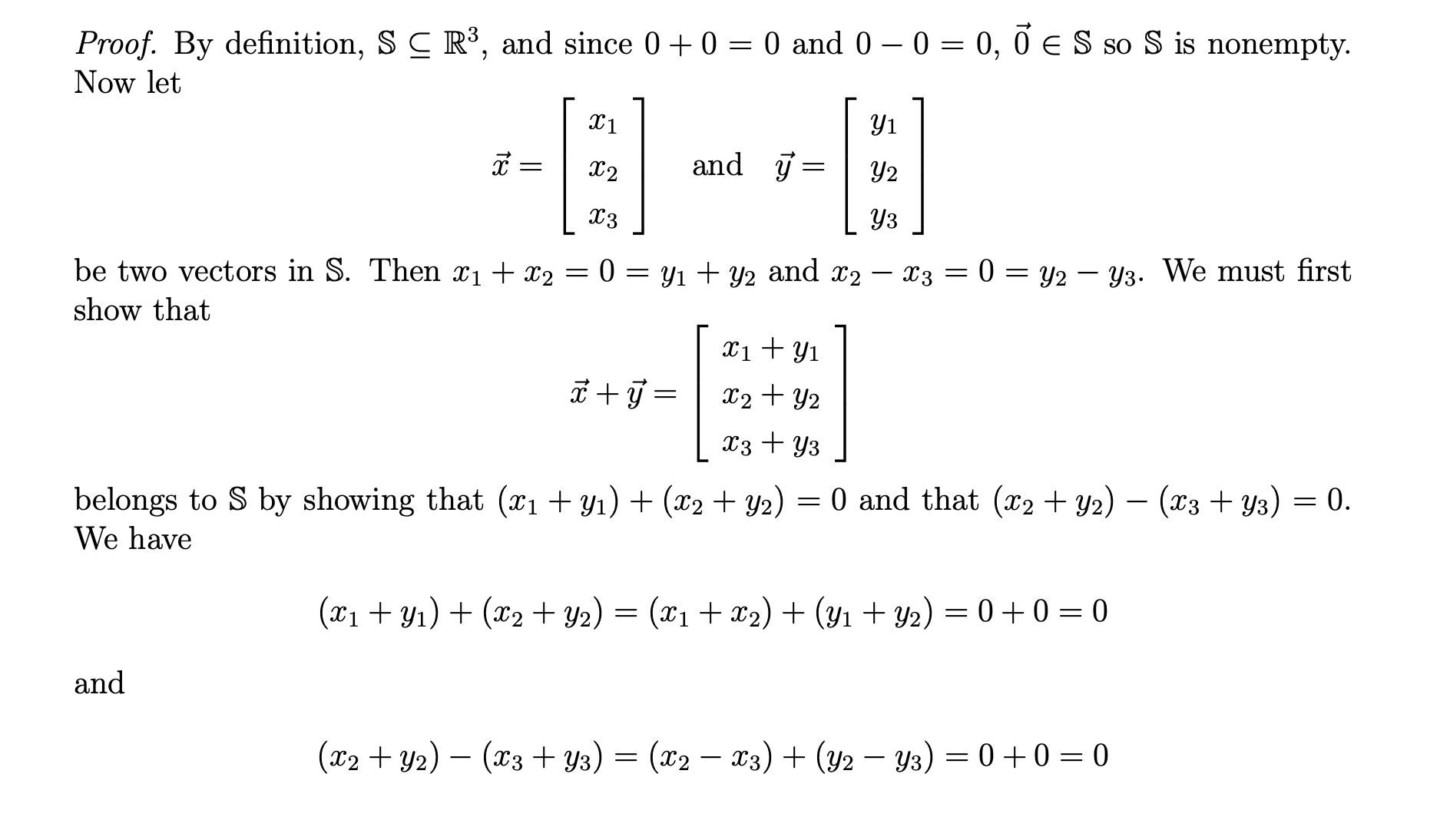Subspace

Definition: A subset $\mathbb{S}$ of ${\mathbb{R}}^n$ is a subspace of ${\mathbb{R}}^n$ if for every $w,x,y\in \mathbb{S}$ and $c,d\in \mathbb{R}$ we have that the 10 axioms hold:

1. S is closed under addition $\vec{x}+\vec{y}\in S$
2. Addition is commutative$\vec{x}+\vec{y}=\vec{y}+\vec{x}\in S$
3. Addition is associative $(\vec{x}+\vec{y})+\vec{w}=\vec{x}+(\vec{y}+\vec{w})$
4. Zero vector $\exists \vec{0}\in \mathbb{S}\text{such that}\vec{v}+\vec{0}=\vec{v}\text{for every}\vec{v}\in \mathbb{S}$
5. Additive Inverse $\text{For each }\vec{x}\in \mathbb{S}\text{ there exists a }(-\vec{x})\in \mathbb{S}\text{ such that }\vec{x}+(-\vec{x})=\vec{0}$
6. $\mathbb{S}$ is closed under scalar multiplication $c\vec{x}\in \mathbb{S}$
7. Scalar multiplication is associative $c(d\vec{x})=(cd)\vec{x}$
8. Distributive law $(c+d)\vec{x}=c\vec{x}+d\vec{x}$
9. Distributive law $(c+d)\vec{x}=c\vec{x}+d\vec{x}$
10. Scalar multiplication identity $1\vec{x}=\vec{x}$

Subspace vs. Subset

Subspace is contained in a space, and subset is contained in a set.

• A subset is some of the elements of a Set
• A subspace is a baby set of a larger father Vector Space

Subspace test

Let $\mathbb{S}$ be a nonempty subset of ${\mathbb{R}}^n$. If for every $\vec{x},\vec{y}\in \mathbb{S}$ and for every $c\in \mathbb{R}$, we have that $\vec{x}+\vec{y}\in \mathbb{S}$ and $c\vec{x}\in S$, then $\mathbb{S}$ is a subspace of ${\mathbb{R}}^n$.

Related

• Vector Space