Volumes of Solids of Revolution

Rotation about Horizontal Axis

Volumes by Disks

This is the simplest case. 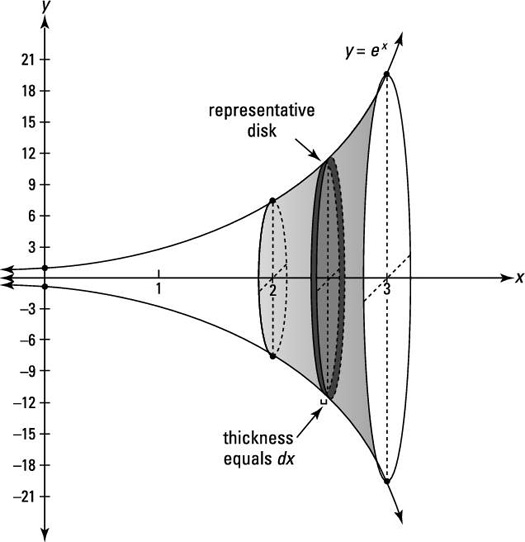Since $dV=\text{ (area of face) (thickness)}$, we have that $V=\int dV$ $V={\int }_a^b\pi [f(x){]}^{2}dx$

Volumes by Washer

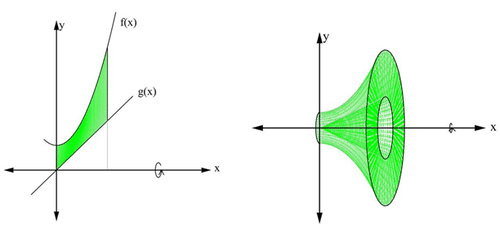This is an extension of the disc method, where $V=\int dV$, but now we are dealing with a hollowed object. $dV=(\pi r_{outer}^2-\pi r_{inner}^2)dx$

In the case the line is down by $k$, we have that $dV=\pi ((f(x)+k{)}^2-k^2)dx$

We have that

Rotation about Vertical Axis

Volumes by Shells

In some cases, volumes of rotation are not conveniently described by the disk method. In these cases, we use the shell method.

$dV=\pi r_{outer}^{2}h-\pi r_{inner}^{2}h$ $dV=\pi [2xdx+(dx{)}^2]f(x)$ Since $(dx{)}^2$ is infinitesimally small, we can ignore that value. $V=\int dV$ $V={\int }_a^{b}2\pi xf(x)dx$