Oldest Self-Balancing Binary Search Tree invented

AVL Tree

Learned in CS240.

An AVL Tree is a BST with an additional height-balance property at every node: $\text{The heights of the left and right subtree differ by at most 1.}$

Important

The height of an empty tree is defined to be $-1$.

If node $v$ has left subtree $L$ and right subtree $R$, then $balance(v):=height(R)-height(L)\in \{-1,0,1\}$

• $balance(v)=-1$ means $v$ is left-heavy
• $balance(v)=+1$ means $v$ is right-heavy

Theorem

An AVL tree on $n$ nodes has $\Theta (\log n)$ height. search, insert, delete all cost $\Theta (\log n)$ in the worst case!

• See Tree Rotation

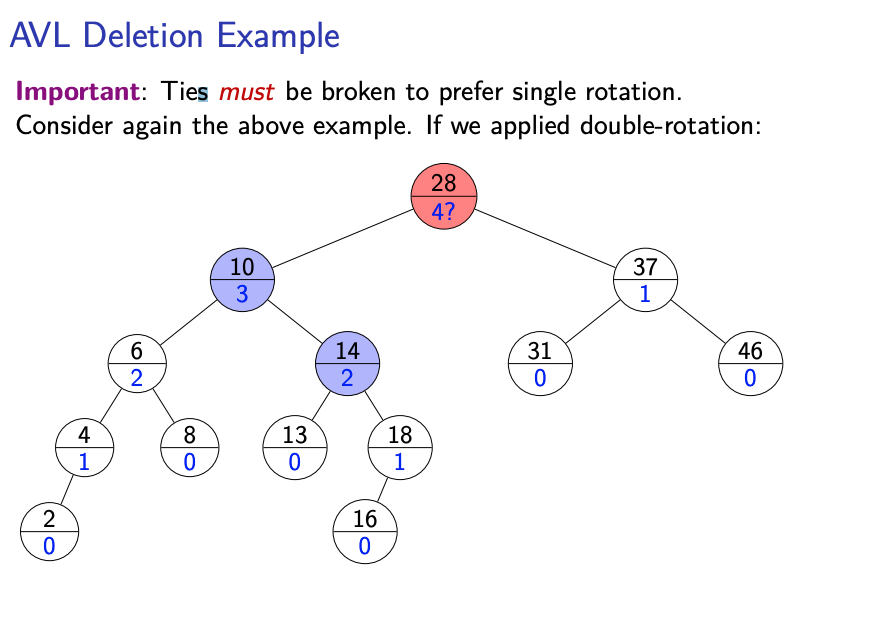
In the case of ties

VERY IMPORTANT: Ties must be broken to prefer single rotation. There are scenarios where if we don’t prefer the single rotation, applying double rotation does not result in a valid AVL tree afterwards.

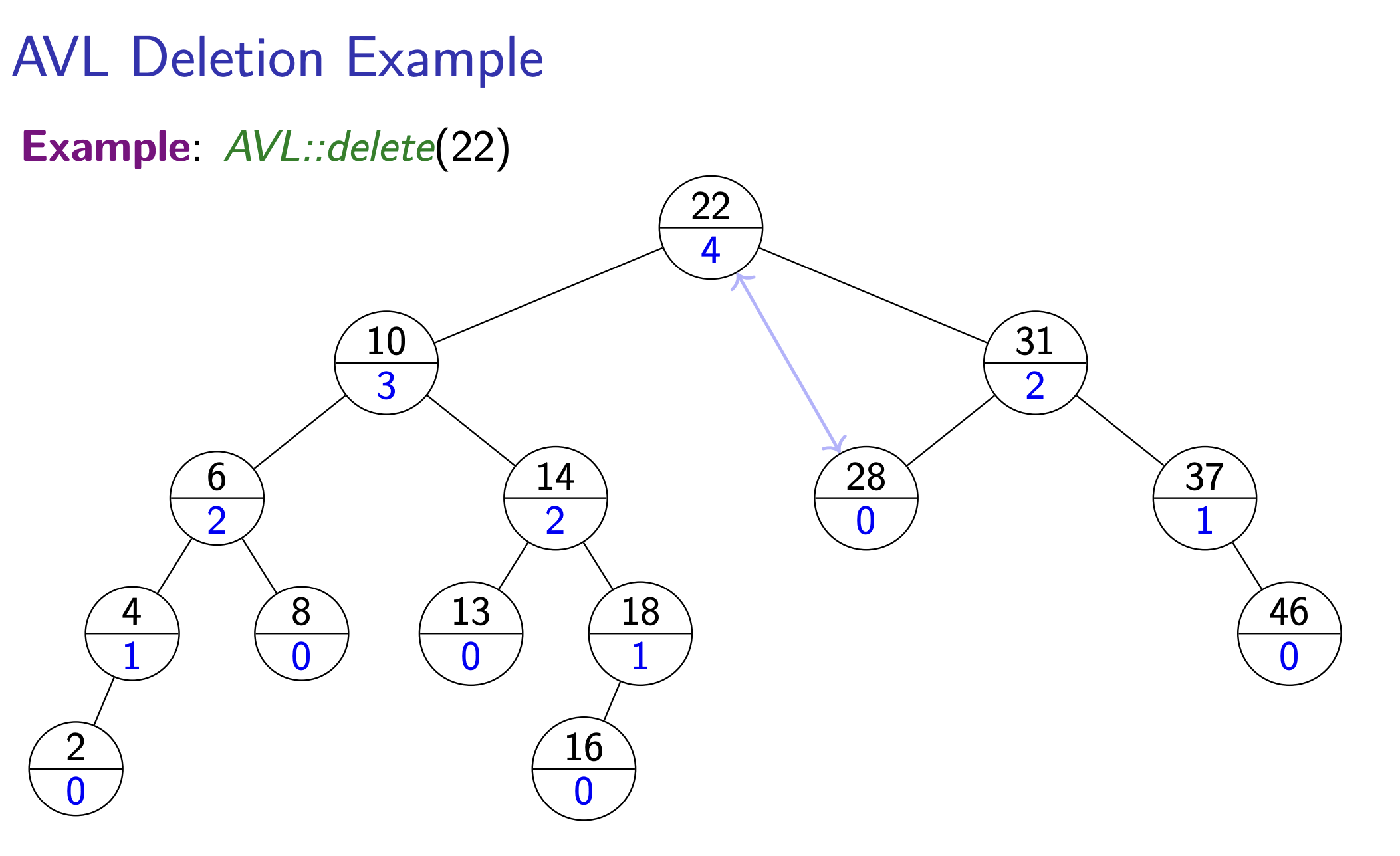
• Note here: the parent here on line 2 refers to the parent of the node with value $k$ after the swap. Like in the example below, calling delete 22, we get the min key of the right subtree, do the swap, and then the parent will be the node with key $31$.

AVL Tree Operations Runtime

Related

• Red-black Tree