Binary Tree

Binary Search Tree (BST)

It is a special kind of Binary Tree that uses comparable keys to assign which direction a child is.

• Left child key < parent node key
• Right child key > parent node key
• There can be no duplicate node

BST invariant: for ALL subtrees, max(left subtree) < root < min(right subtree)

Time Complexity

Assuming the tree is pretty balanced.

• Indexing: Binary Search Tree: $O(\log n)$
• Search: Binary Search Tree: $O(\log n)$
• Insertion: Binary Search Tree: $O(\log n)$

Implementation

Some of the functions with a BST are a little hard to grasp for me, because I need to use recursion.

Inserting and searching is fairly easy. You always insert at the end of the tree, not in the middle of tree.

Checking WellFormedness CS138 Final

We need to recursively check four things:

• this→left→key < this→key
• this→right→key > this→key
• this→maxLeft()→key < this→key
• this→minRight()→key > this→key

bool BST_Node::isWellformed() const {
    // TODO - This is for you to implement. BST::isWellformedBST has been provided for you.
	if (nullptr != this->left) {
		assert(this->left->key < this->key);
		assert(this->maxLeft()->key < this->key);
		//Recursively check the left node
		this->left->isWellformed();
	}
	if (nullptr != this->right) {
		assert(this->right->key > this->key);
		assert(this->minRight()->key > this->key);
		// Recursively check the right node
		this->right->isWellformed();
	}
	
	return true; //No assertions tripped, return true
}

Ahh, so I've already done this before.

There is this LeetCode question, which I haven’t done yet. https://leetcode.com/problems/validate-binary-search-tree/submissions/

BST Deletion

Option 1 (BAD)

Add a boolean “zombie” flag to each node

• Zombie nodes are not printed
• Advantage is that it’s simple, but disadvantage long term performance degrades as tree is full of zombies

Option 2 (TO USE)

You handle three cases with the target node to delete. Case 1: If the target node has no children, just delete it Case 2: If the target node has a single children, link target node’s parent to target node’s children, and delete the target node Case 3: Either with the max of the left subtree, or the min of the right subtree (guaranteed to only have 0 or 1 child, not 2 children by definition)

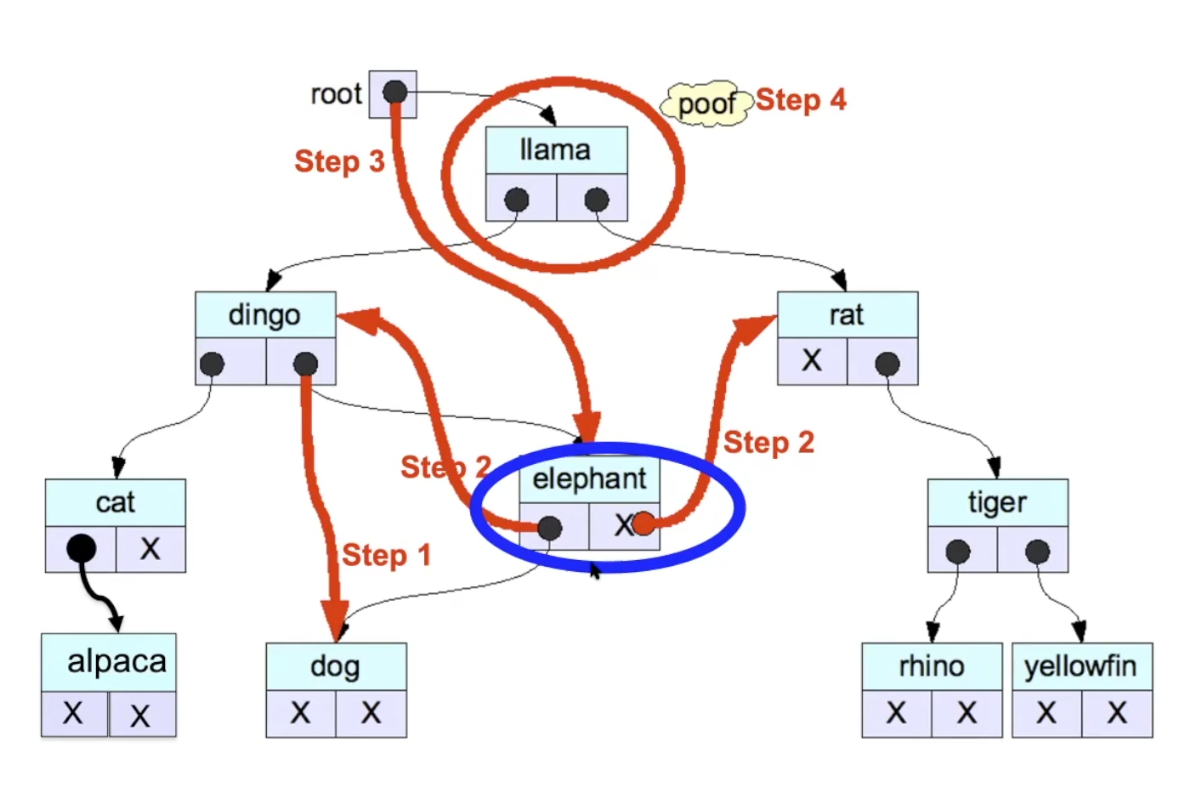
Example with Case 3

Circled in red is the target node. Circled in blue is the replacement node.

1. Find replacement node, and link replacement node’s parent to replacement node’s child (only should have one)
   1. In our case, we will decide the replacement node as the max down the left subtree of the target node.
2. Insert replacement node in place of target node by updating the pointers
3. update the pointer of parent of target node to the replacement node
4. Delete target node

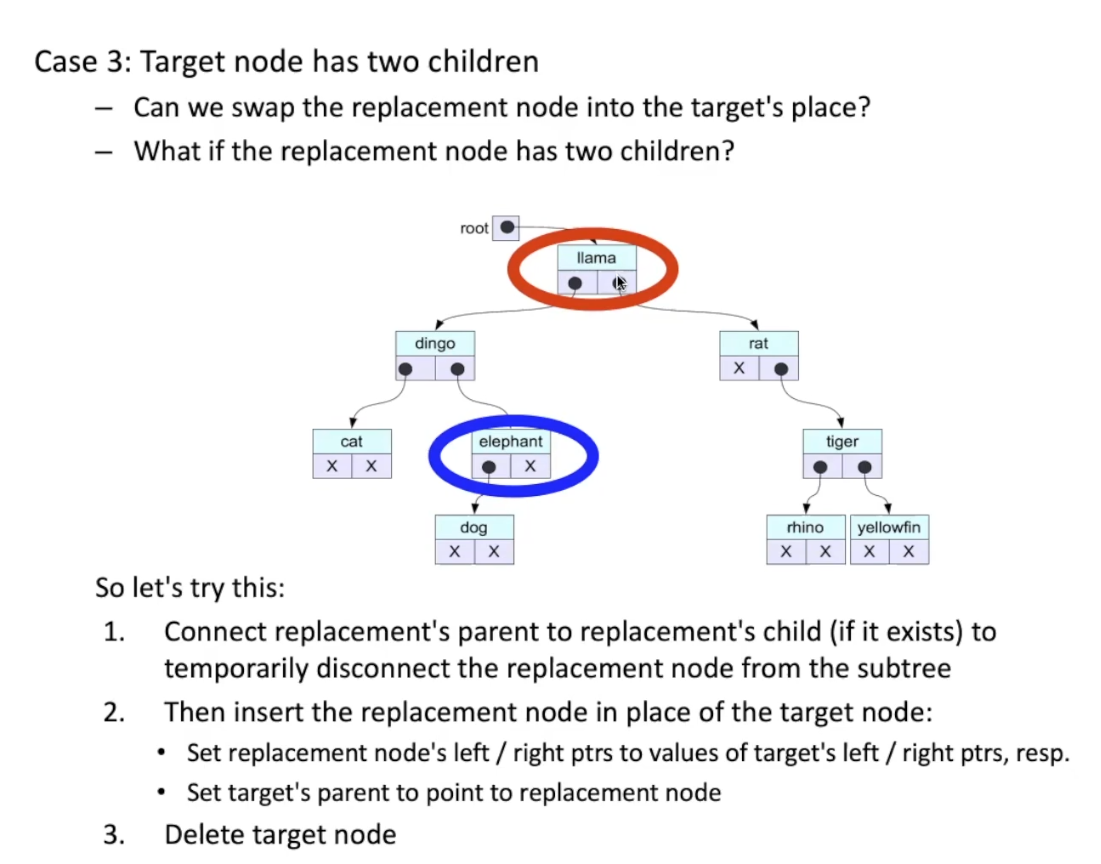
The image below is a little confusing

Option 3 (SLOW)

Copy over, and then delete a single node.

BST Range Search

Learned in CS247.

Related

• Tree Traversal
• Self-Balancing Binary Search Tree