Variance

Covariance

Learned this in Statistics. when the random variables are independent, the covariance is 0, since $E[XY]=E[X]E[Y]$ (see full formula below).

We use the covariance to get a measure of the Correlation (i.e. Covariance is used to calculate the Correlation Coefficient).

Covariance

Covariance describes how much two variables vary together. Covariance is short for correlated variances.

The covariance of two random variables $X,Y$ is $Cov(X,Y)={\sigma }_{xy}=E[(X-E(X))\cdot (Y-E(Y))]$ This can also be written as $Cov(X,Y)=E(XY)-E(X)\cdot E(Y)$

• This is the”difference between the average of the products and the product of the averages”

Warning

NOTE: The covariance can be negative.

A Simple example is suppose:

• X = # hours spent playing video games
• Y = grade on STAT206 final

If $X>E(X)$, you expect $Y<E(Y)$, so $Cov(X,Y)<0$

The covariance of a random variable with itself is just the variance of that random variable.

Variance vs covariance: $Var(X)=E[(X-E(X){)}^2]$ $Cov(X,Y)=E[(X-E(X))\cdot (Y-E(Y))]$

Correlation vs. covariance?

The correlation is computed using the covariance. Correlation allows prediction. If you are significantly taller than me I can predict that you also weigh more than me.

Properties of Covariance

1. $Cov(X,k)=0$, where $k$ is a constant
2. $Cov(X,X)=Var(X)$
3. $Cov(X,Y)=Cov(Y,X)$
4. $Cov(X,a+bX)=bVar(X)$
5. $X$ and $Y$ are independent $⟹Cov(X,Y)=0$
   1. However, $Cov(X,Y)=0$ does NOT imply $X$ and $Y$ are independent
6. $Cov(X,Y+Z)=Cov(X,Y)+Cov(X,Z)$

Other

Varying the covariance while holding the variance constant:

• Source: https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/05-Multivariate-Gaussians.ipynb

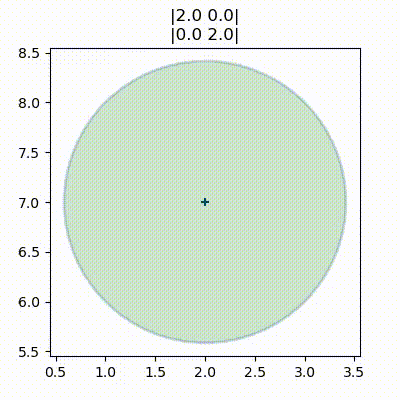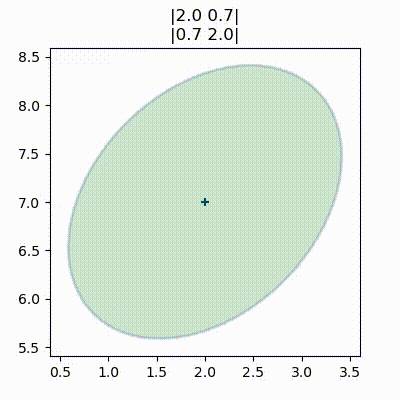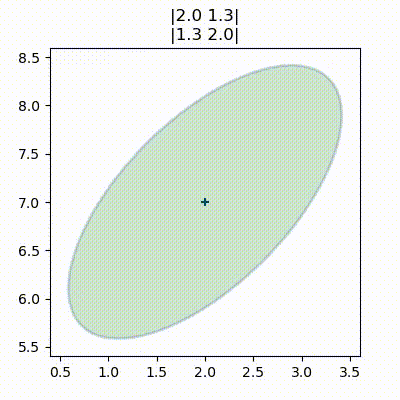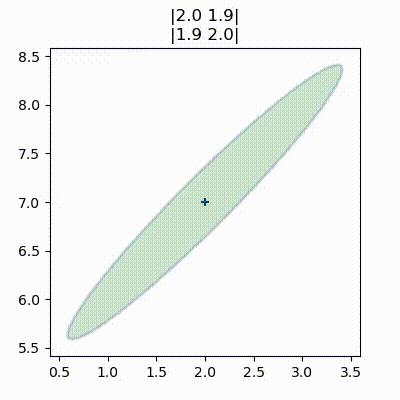
These are called error/confidence ellipses. They’re very useful to visualize the correlation

To build intuition, think of this image

Related

• Correlation
• Covariance Matrix