Entropy (Information Theory)

Entropy quantifies uncertainty.

In information theory, the entropy of a random variable is the average level of “information”, “surprise”, or “uncertainty” inherent to the variable’s possible outcomes.

Given a discrete random variable $X$, which takes values in the alphabet $\mathcal{X}$ and is distributed according to $p:\mathcal{X}\to [0,1]$:

$\mathrm{H}(X)=\mathbb{E}[-\log p(X)]$ $H(X)=-{\sum }_{x\in X}p(x)\log p(x)$

• Cross-Entropy is this, but comparing $p(x)$ to $q(x)$!!

Entropy

Entropy = measure of uncertainty over random Variable X = number of bits required to encode X (on average)

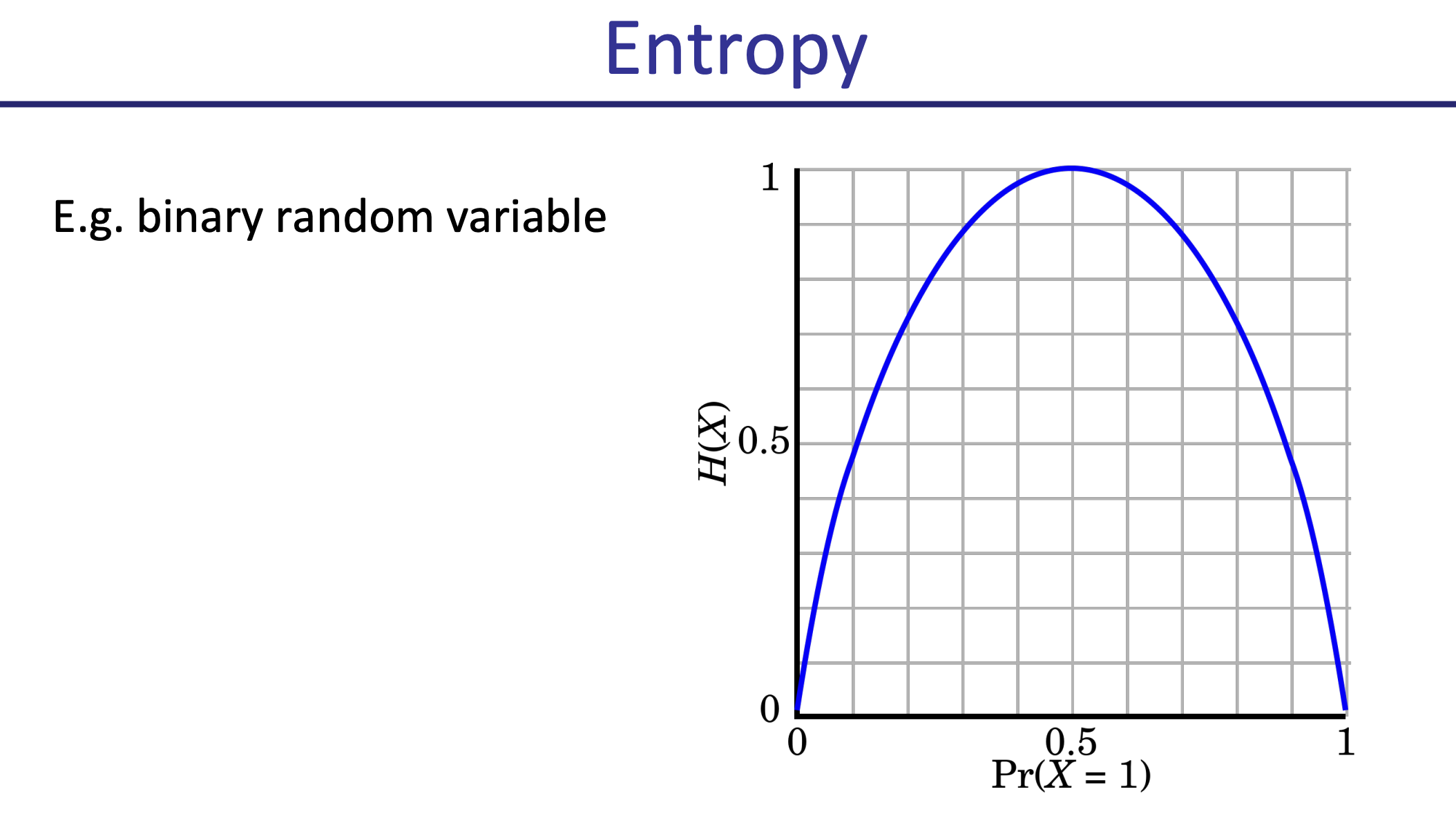
• The more spread out your data, the higher the entropy.

Why log??

Claude Shannon showed that if you want a function that satisfies some intuitive properties of “information”, it must be proportional to the logarithm → See Fundamental Properties of Information

Entropy vs. variance?

Variance measures the spread of values, whereas entropy measures the uncertainty in outcomes. You can have:

• high variance but low entropy (e.g., when a distribution has rare but extreme outliers).
• High entropy but low variance (e.g., when outcomes are uniformly likely in a small range).

Entropy should be a measure of how “surprising” the average outcome of a variable is. For a continuous random variable, differential entropy is analogous to entropy.

From Sinkhorn Divergence

I have yet to fully understand this. It seems to be something with making the function Convex?

The entropy of a matrix is given by $H(P)=-{\sum }_{ij}{P}_{ij}\log P_{ij}$ Low entropy = sparse matrix, i.e. most of non-zero values c are concentrated in a few points. The lower the entropy, the closer we are approximating to the original solution for the EMD.

Related

• Maximum Entropy
• Constrained Optimization