Markov Process

Related to Markov Chain.

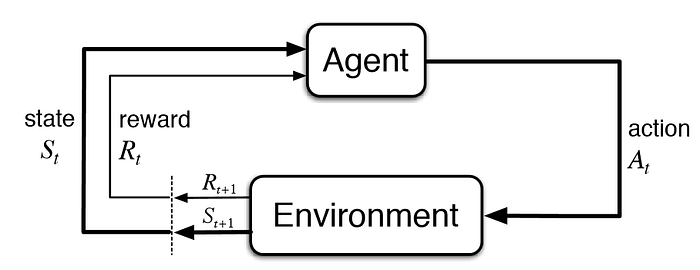
Markov decision processes formally describe an environment for reinforcement learning where the environment is fully observable

• i.e. The current state completely characterizes the process
• Almost all RL problems can be formalized as MDPs, e.g.
  • Optimal control primarily deals with continuous MDPs
  • Partially observable problems can be converted into MDPs
  • Bandits are MDPs with one state

Markov Property

Definition

A state $S_t$ is Markov if and only if $\mathbb{P}[S_{t+1}|S_t]=\mathbb{P}[S_{t+1}\mid S_1,\dots ,S_t]$ i.e. the state captures all relevant information from the history

• “The future is independent of the past given the present”
• Once the state is known, the history may be thrown away
• i.e. The state is a sufficient statistic of the future

State Transition Probability

“What is the probability of transitioning from state $s$ to state $s^{\prime }$?”

For a Markov state $s$ and successor state $s^{\prime }$ , the state transition probability is defined by $\mathcal{P}s{s}^{\prime }=\mathbb{P}[S_{t+1}=s^{\prime }|S_t=s]$

State transition matrix $\mathcal{P}$ defines transition probabilities from all states $s$ to all successor states $s^{\prime }$, where $\mathcal{P}=\left[\begin{array}{ccc}{\mathcal{P}}_{11}& \dots & {\mathcal{P}}_{1n}\\ ⋮& & ⋮\\ {\mathcal{P}}_{n1}& \dots & {\mathcal{P}}_{nn}\end{array}\right]$

Markov Process / Markov Chain

At a high level, a Markov process is a sequence of random states $S_1,S_2,\dots$ with the Markov property.

Definition

A Markov Process is a tuple $⟨\mathcal{S},\mathcal{P}⟩$

• $\mathcal{S}$ is a finite set of states
• $\mathcal{P}$ is a state transition probability matrix, ${\mathcal{P}}_{s{s}^{\prime }}=\mathbb{P}[S_{t+1}=s^{\prime }\mid S_t=s]$

$\mathbb{P}$ stands for probability.

Markov Reward Process

A Markov reward process is a Markov process with rewards (values for each state).

Definition

A Markov Reward Process is a tuple $⟨\mathcal{S},\mathcal{P},\mathcal{R},\gamma ⟩$

• $\mathcal{S}$ is a finite set of states
• $\mathcal{P}$ is a state transition probability matrix, ${\mathcal{P}}_{s{s}^{\prime }}=\mathbb{P}[S_{t+1}=s^{\prime }\mid S_t=s]$
• $\mathcal{R}$ is a reward function, $R_s=\mathbb{E}[R_{t+1}\mid S_t=s]$
• $\gamma$ is a discount factor, $\gamma \in [0,1]$

$\mathbb{P}$ stands for probability, while $\mathbb{E}$ stands for expected.

• Return
• Discount Factor
• Value Function

We can solve the MRP analytically, using the fact that we know this is a Markov Process. So we break down the value function into: Value = (immediate reward) + (discounted sum of future rewards) $V=R+\gamma PV$ We know both $R$ and $P$, and we set $\gamma$ ourselves, so we can solve for $V$ directly. $V=R(I-\gamma P{)}^{-1}$ For analytical way, we can directly solve MRP, which takes around $O(N^3)$ where $N$ is the number of states, and solve the matrix.

We can also use iterative algorithm with Dynamic Programming using a similar idea as the Dynamic Programming using a similar idea as the Bellman Equation.

• Initialize $V_0(s)=0$ for all $s$
• For $k=1$ until convergence (i.e. $|v_k-v_{k-1}|<ϵ$)
• $\forall s\in S$, $V_k(s)=R(s)+\gamma {\sum }_{s^{\prime }\in S}P(s^{\prime }|s)V_{k-1}(s^{\prime })$

Markov Decision Process

Now, we add decisions. A MDP is a MRP with decisions.

Definition

A Markov Decision Process is a tuple $⟨\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma ⟩$

• $\mathcal{S}$ is a finite set of states
• $\mathcal{A}$ is a finite set of actions
• $\mathcal{P}$ is a state transition probability matrix, ${\mathcal{P}}_{s{s}^{\prime }}^a=\mathbb{P}[S_{t+1}=s^{\prime }\mid S_t=s,A_t=a]$
• $\mathcal{R}$ is a reward function, $R_s^a=\mathbb{E}[R_{t+1}\mid S_t=s,A_t=a]$
• $\gamma$ is a discount factor, $\gamma \in [0,1]$

The goal is to find the Optimal Policy, which maximizes the expected return.

• Policy
• Value Function

If you have a MDP + a policy, that just becomes a MRP. So can solve using the technique above.

Also see Partially Observable Markov Decision Process

MDPs are everywhere

• Cleaning Robot
• Walking Robot
• Pole Balancing
• Tetris
• Backgammon
• Server management
• Shortest path problems
• Model for animals or people

Solving MDPs

To solve MDPs, we use Dynamic Programming in Reinforcement Learning.

• Value Iteration
• Policy Iteration

Maximum Entropy MDP

Regular formulation ${\max }_{\pi }E\left[{\sum }_{t=0}^H{r}_t\right]$

Maximum-entropy formulation ${\max }_{\pi }E\left[{\sum }_{t=0}^H{r}_t+\beta H(\pi (\cdot |s_t))\right]$

Continuous MDPs with Discretization

Value iteration becomes impractical when the state space $S$ is continuous.

• Solution one is to Discretization

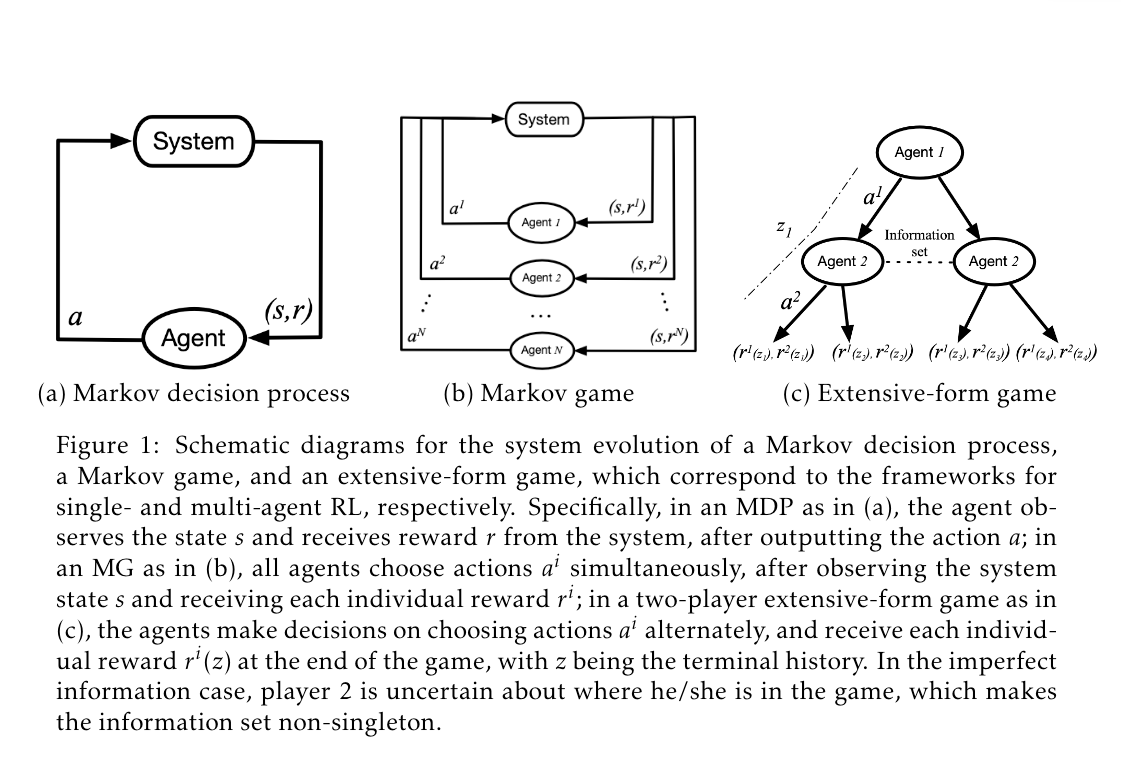
Extending MDPs

From page 7 of this paper, you have

• Markov Game
• Extensive-Form Game