Epipolar Geometry

Learned from Cyrill Stachniss.

Epipolar geometry deals with the geometric relationship between two views of the same scene captured by different cameras or from different viewpoints.

Resources

• Epipolar Geometry Basics (Cyrill Stachniss)
  • slides here
• https://docs.opencv.org/4.x/da/de9/tutorial_py_epipolar_geometry.html

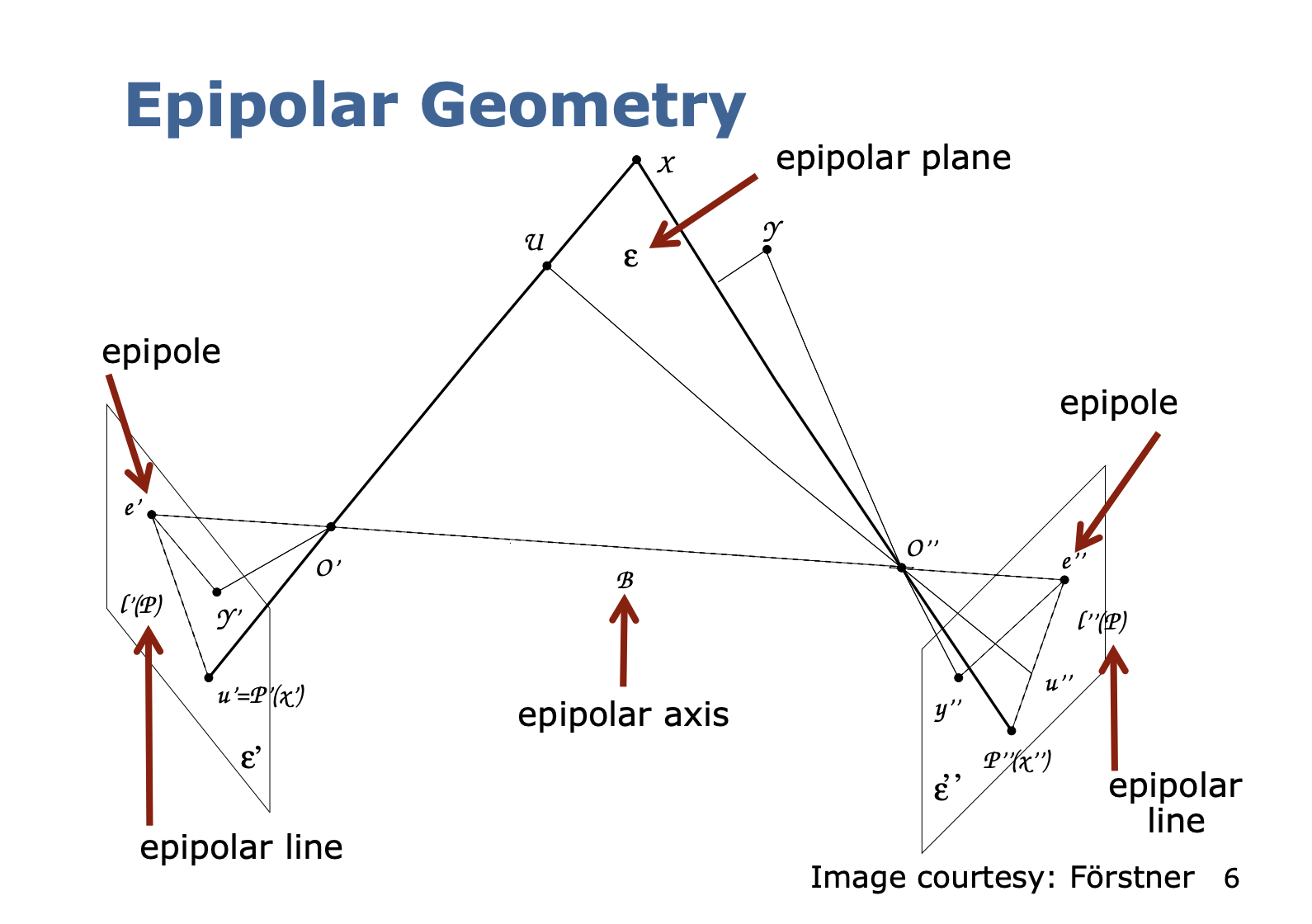
• It’s a little hard to visualize, but you should be able to see the epipolar plane being slanted up

Epipolar axis is line connecting the two camera projection centers

• Isn’t this the same as baseline $b$, which we use for the Fundamental Matrix?

Epipolar plane is the plane spanned by $O,O^{\prime \prime }$and $x$

• Different sets of points leads to different epipolar planes

Epipoles are the projection of the other camera’s projection center into the image.

• Basically intersection of epipolar axis and the image plane

Epipolar line is the intersection of the epipolar plane and the image plane.

• You can also think of it as the line that connects the epipole and the projected point

The epipolar plane is fundamental

All the points lie in the epipolar plane. This simplifies the task of predicting the location of corresponding a point in the other image.