Tree Data Structure

Fenwick Tree

A Fenwick/Binary-Indexed tree can both process range sum queries and update values real-time in $O(\log n)$.

I still don’t fully grasp why it works, but I grasp the algorithm.

Resources

• Episode 0 - Fenwick Trees by Algorithms Live!
• Fenwick Tree range queries

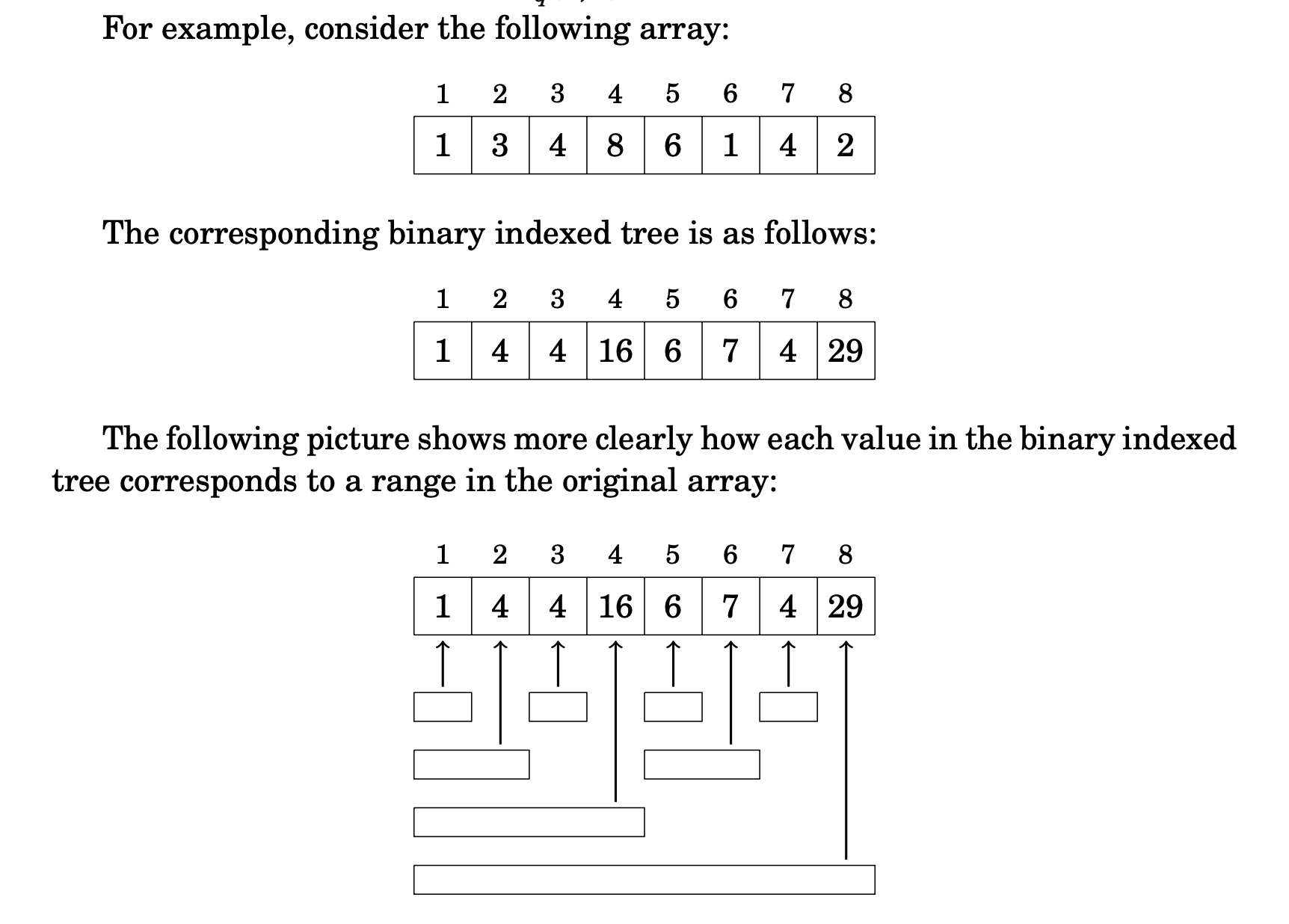
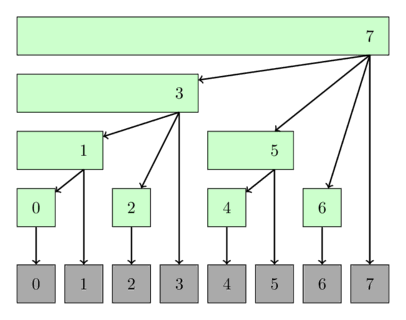
To process a query, we use this formula: $p(k)=k\&-k$ which gets the rightmost set bit of $k$.

1. Add $tree[k]$ to a running sum
2. Decrement $k$ by $p(k)$, which subtracts its rightmost set bit
3. Repeat until $k$ reaches 0
4. Return the running sum

Where does k \& -k come from??

That gives the rightmost set bit.

To update a value at index i, we only update certain indices of the tree:

1. Update $tree[i]$
2. Increment $i$ by $p(i)$
3. Repeat until $i$ is out of bounds, i.e. while $i\le n$

Implementation (1-indexed)

This is the default implementation that supports range queries and point updates.

int sum(int k) { 
	int s = 0; 
	while (k > 0) { 
		s += tree[k]; 
		k -= k&-k; 
	} 
	return s;
}
 
int range_sum(int l, int r) {
	return sum(r) - sum(l-1);
}
 
void update(int i, int x) { 
	while (i <= n) { 
		tree[i] += x; 
		i += i&-i; 
	} 
}

• Taken from CP Handbook

From ChatGPT with a struct (basically the same), but clean isolated

struct Fenwick {
    int n;
    vector<long long> bit;
    Fenwick(int n) : n(n), bit(n + 1, 0) {}
 
    void add(int i, long long delta) {
        for (; i <= n; i += i & -i) bit[i] += delta;
    }
 
    long long sum(int i) {
        long long res = 0;
        for (; i > 0; i -= i & -i) res += bit[i];
        return res;
    }
 
    long long rangeSum(int l, int r) {
        if (l > r) return 0;
        return sum(r) - sum(l - 1);
    }
};

Variants (to master)

The following are variants of Fenwick trees that need extra work.

1. Point Update and Range Query (Default)
2. Range Update and Point Query
3. Range Update and Range Query

Extra

This below is confusing to me, but I think it’s still good information. Each value of $tree[k]$ corresponds to $tree[k]=su{m}_q(k-p(k)+1,k)$

Related

• Segment Tree
• Sparse Table