Data Structure

Tree

A tree is a special kind of directed Graph.

• Root node has no parent
• Each node has 0 or more children

We can sub-categorize trees into:

• N-ary trees
• Binary Tree
• Binary Search Tree

Leaf nodes are nodes that have no children.

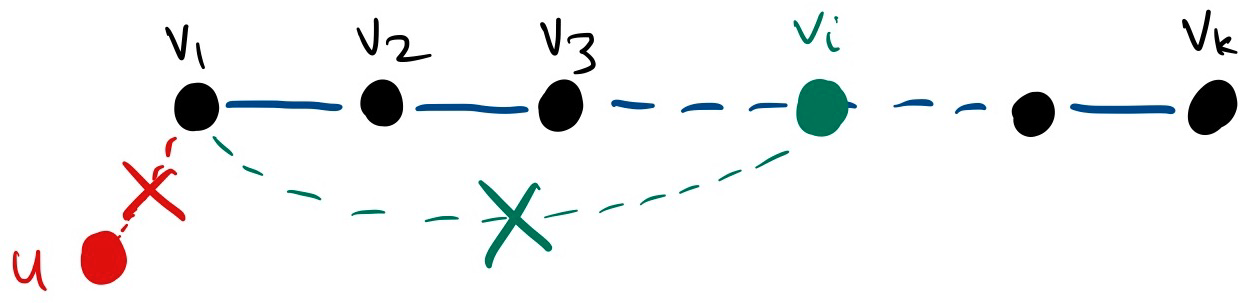
SUPER IMPORTANT PROPERTY: There is only 1 path between any two nodes on the tree. This is not the case with a Graph.

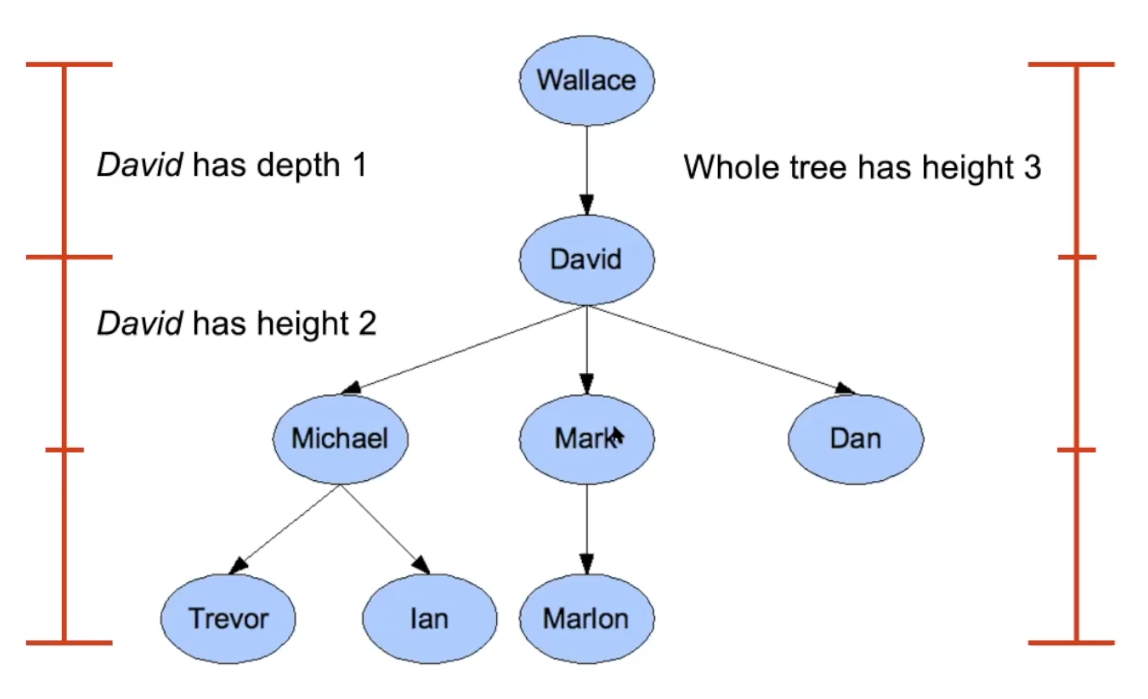
Depth vs. height

Height of a node (looking up from leaf node) → length of the longest path from it down to a leaf

• Leaf node has height 0

Depth of a node (looking down from root) → length of the path from the root to it

• Root has depth 0

Storing Trees as Arrays

It is very common to store trees as arrays. The way they are represented is dependent on the tree.

• Fenwick Tree
• Segment Tree

We also saw this in CS240, storing the Heap as an Array.

Types of Trees

• Segment Tree
• Fenwick Tree
• Spanning Tree
• Suffix Tree
• Disjoint Set Union
• Treap
• Quadtree
• K-d Tree
• Range Tree

Related

• Tree Query

From MATH239

Definitions

Tree

A tree is a Connected Graph with no cycles.

Forest

A forest is a Graph with no cycles.

Leaf

A leaf in a tree is a vertex of degree 1.

A tree is a “minimally-connected graph”: it is connected, but removing any edge disconnects it.

Theorems and Lemmas There are all these theorems and lemmas that you should be able to prove.

Lemma 5.1.3

Let $x,y$ be vertices in a tree $T$. Then there exists a unique $x,y$-path in $T$.

Lemma 5.1.4

Every edge in a tree or forest is a bridge.

Theorem 5.1.5.

If $T$ is a tree, then $|E(T)|=|V(T)|-1$.

Theorem 5.1.8

If $T$ is a tree with at least two vertices, then it has at least two leaves.

Lemma 3

Every tree is bipartite.

Related

• Spanning Tree