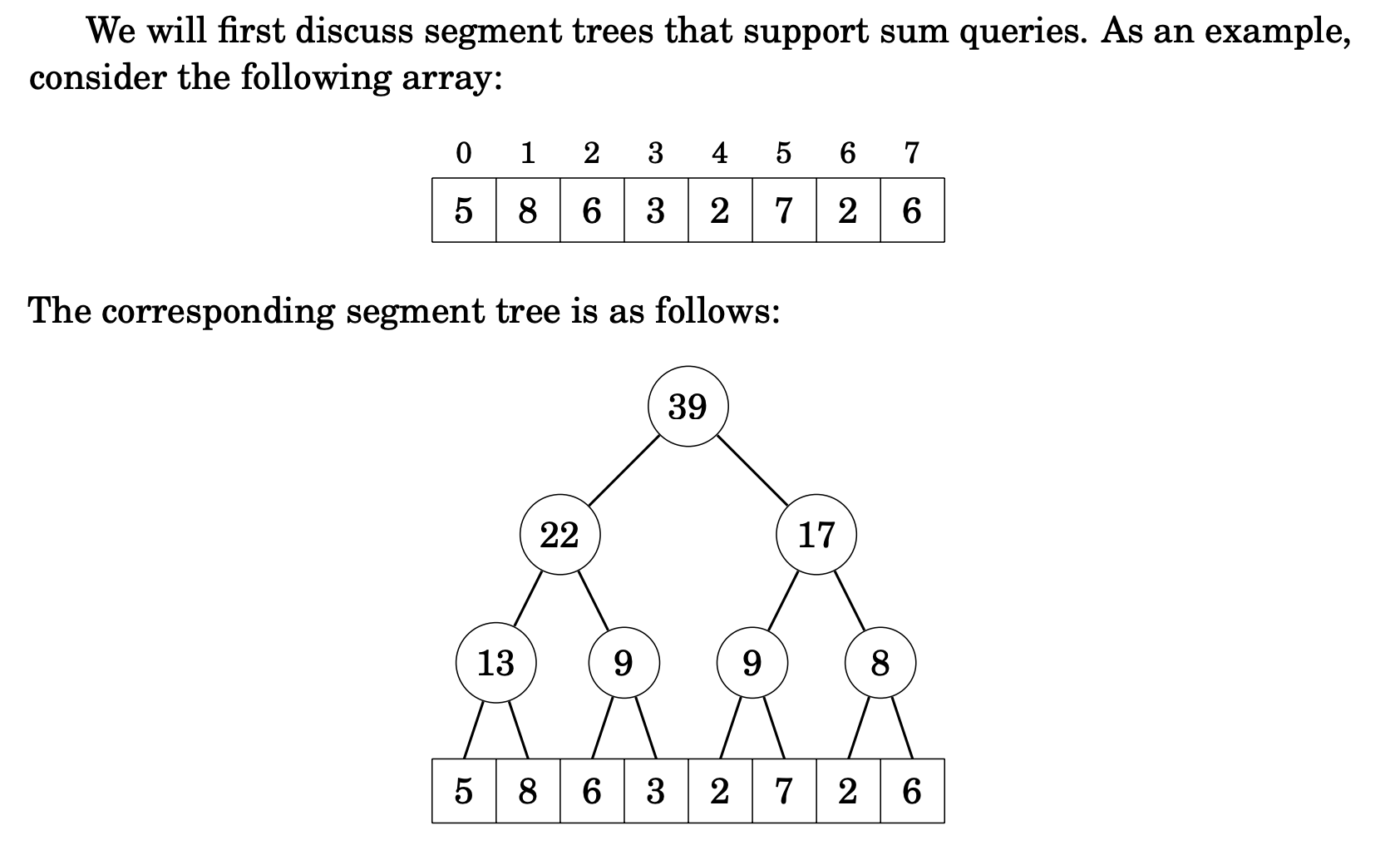
Segment Tree
A segment tree is typically used to store a set of intervals, such as the start and end times of events or the positions of objects in a two-dimensional space.
- Each node in the tree represents a particular interval, and the children of a node represent sub-intervals of the parent interval
- Allows for efficient querying and updating of the data, as the tree can be searched and traversed to find the relevant intervals.
This is a segment tree problem that I couldn’t do at a contest:
Resources:
- https://cp-algorithms.com/data_structures/segment_tree.html
- Segment Tree (Implementation) by Errichto
- Segment Tree by Algorithms Live
4*Nor2*N?Eric Pei reports 4N to be faster https://ericpei.ca/posts/segment-tree/
Todo problems:
A Segment Tree is a more general Fenwick Tree that can support other queries (more than range queries), such as a Range Minimum Query (RMQ).

Time complexity analysis
When I was trying my own analysis, I was confused how it could be , and not , since there is a case where both the left and right subtrees need to be visited. So in the worst case, the entire tree is visited, and thus a query takes time.
The proof is that you can show that at most 4 vertices are visited per level. Since there are levels, then the runtime is .
“Let’s assume that we visit three or four vertices in the current level.”
First, observe that these 4 vertices must be contiguous, because we are computing the sum for a contiguous range.
Then, you see that these 2 middle vertices are completely covered, so there is no point of exploring down. Assume by contradiction that it isn’t completely covered. Then, the left most node would be disjoint. You would end up querying a non-contiguous interval.
From those vertices, we will analyze the vertices in the middle more carefully. Since the sum query asks for the sum of a continuous subarray, we know that segments corresponding to the visited vertices in the middle will be completely covered by the segment of the sum query. ”
Number of nodes
See Binary Tree.
Implementation
Erichto gave a really good visualization, see it as a binary tree.
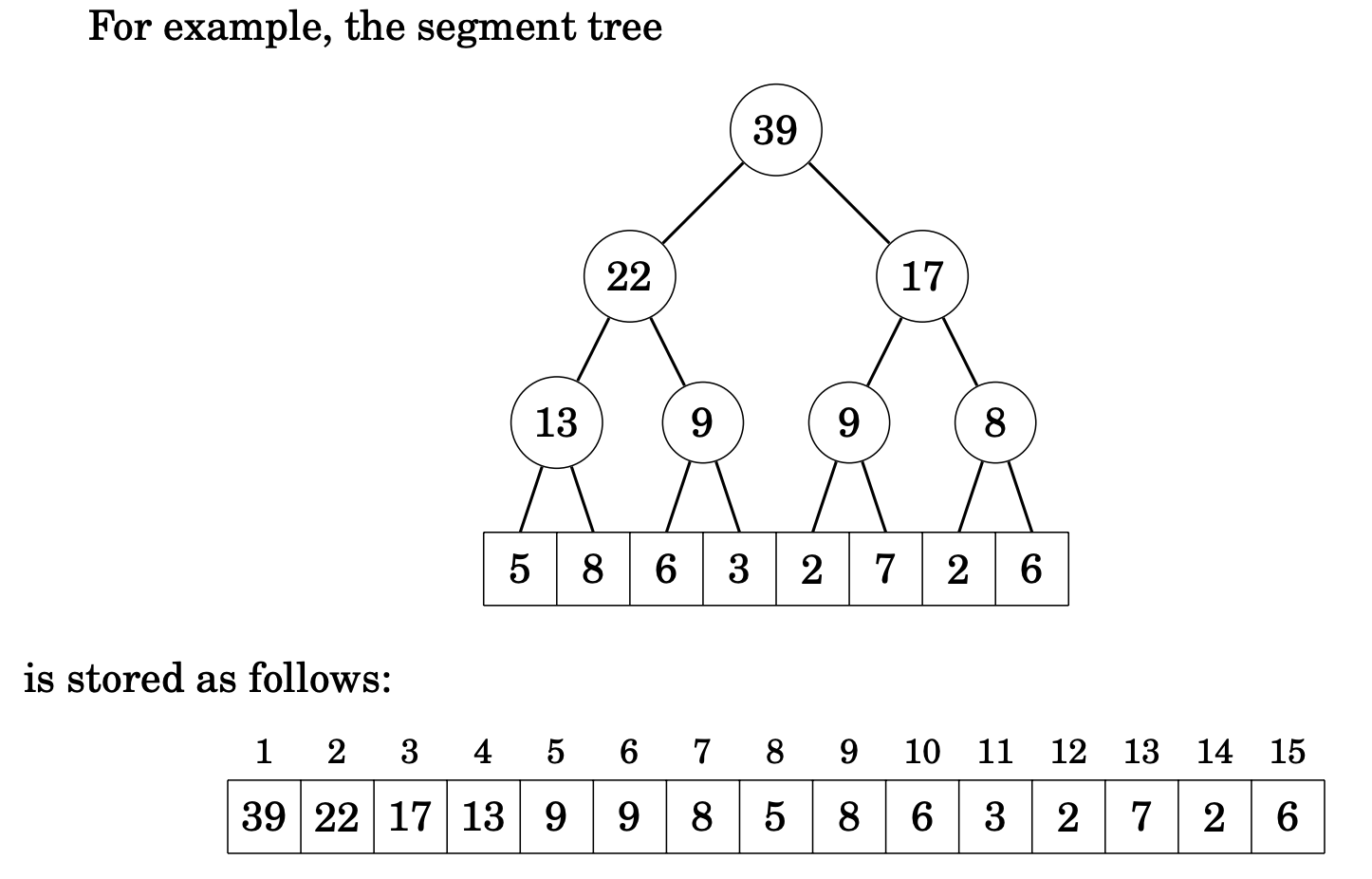
We store a segment tree as an array of elements where is the size of the original array and a power of two.
The tree nodes are stored from top to bottom:
tree[1]is the top node,tree[2]andtree[3]are its children, and so ontree[n]totree[2n−1]correspond to the values of the original array on the bottom level of the tree
Warning
The above statement is only true when for some
When it’s not a perfect power of 2, it will be slightly different.
To access the child and parents:
- Parent: the parent of tree[k] tree[k/2]
- Children: tree[k] tree[2k] and tree[2k+1]
- even = left child
- odd = right child
We always want to be on the left child node for the left side, and right child node on the right side so that the parent is representative.
Why use 1-indexing?
When we do Heap as an array, it seems to be 0-indexed. Both work. If you do 0-indexed,you need to use instead of to get the children node.
There’s a template by CP Handbook, but I found it pretty confusing. Use the one by cp-algorithms
int t[4*MAXN];
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = a[tl];
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
t[v] = t[v*2] + t[v*2+1];
}
}
int sum(int v, int tl, int tr, int l, int r) {
if (l > r)
return 0;
if (l == tl && r == tr) {
return t[v];
}
int tm = (tl + tr) / 2;
return sum(v*2, tl, tm, l, min(r, tm))
+ sum(v*2+1, tm+1, tr, max(l, tm+1), r);
}
void update(int v, int tl, int tr, int pos, int new_val) {
if (tl == tr) {
t[v] = new_val;
} else {
int tm = (tl + tr) / 2;
if (pos <= tm)
update(v*2, tl, tm, pos, new_val);
else
update(v*2+1, tm+1, tr, pos, new_val);
t[v] = t[v*2] + t[v*2+1];
}
}Segment tree as a class, saw from this submission https://codeforces.com/contest/2050/submission/295083798
#include <bits/stdc++.h>
using namespace std;
#define ull unsigned long long int
#define ll long long
#define pll pair<ll, ll>
#define vll vector<ll>
#define vvll vector<vector<ll>>
#define vvvi vector<vector<vector<ll>>>
#define mll map<ll, ll>
#define all(v) (v).begin(),(v).end()
#define pb push_back
#define sz size()
#define f first
#define s second
#define nl endl
#define MOD 1000000007
#define PI 3.1415926535897932384626433832795
#define INF 1e9
#define min_pq priority_queue<ll, vector<ll>, greater<ll>>
#define init(a,n) for(ll i=0; i<n; i++) { cin>>a[i]; }
#define print(a) for(const auto&i: (a)){cerr<<i<<" ";}cerr<<nl;
class SegmentTree {
vll seg;
ll n;
public:
SegmentTree(ll n) {
this->n = n;
seg.resize(4 * n, 0);
}
void build(const vll &v) {
build(0, 0, n - 1, v);
}
ll query(ll l, ll r) {
return query(0, 0, n - 1, l, r);
}
private:
void build(ll index, ll low, ll high, const vll &v) {
if (low == high) {
seg[index] = v[low];
return;
}
ll mid = low + (high - low) / 2;
build(2 * index + 1, low, mid, v);
build(2 * index + 2, mid + 1, high, v);
seg[index] = gcd(seg[2 * index + 1], seg[2 * index + 2]);
}
ll query(ll index, ll low, ll high, ll l, ll r) {
if (l > high || r < low) return 0;
if (low >= l && high <= r) return seg[index];
ll mid = low + (high - low) / 2;
ll left = query(2 * index + 1, low, mid, l, r);
ll right = query(2 * index + 2, mid + 1, high, l, r);
return gcd(left, right);
}
ll gcd(ll a, ll b) {
while (b) {
ll temp = b;
b = a % b;
a = temp;
}
return a;
}
};
void solve() {
ll n, q;
cin >> n >> q;
vll a(n);
for (ll i = 0; i < n; i++) {
cin >> a[i];
}
if (n == 1) {
while (q--) {
ll l, r;
cin >> l >> r;
cout << "0 ";
}
cout<<nl;
return;
}
vll diff(n - 1);
for (ll i = 0; i < n - 1; i++) {
diff[i] = abs(a[i + 1] - a[i]);
}
SegmentTree segTree(n - 1);
segTree.build(diff);
while (q--) {
ll l, r;
cin >> l >> r;
--l, --r;
if (l == r) {
cout << "0 ";
} else {
cout << segTree.query(l, r - 1) << " ";
}
}
cout<<nl;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
ll t;
cin >> t;
while (t--) {
solve();
}
return 0;
}