Flow Matching

This is what pi0 uses.

Flow matching is a training method used to learn a mapping from a source distribution to a target distribution by approximating the underlying vector field.

• Source: meta guide

The paper:

• https://arxiv.org/pdf/2210.02747

Resources

• https://arxiv.org/pdf/2412.06264 (Flow matching guide and code by meta)
• https://flowreinforce.github.io/
• https://mlg.eng.cam.ac.uk/blog/2024/01/20/flow-matching.html
• https://diffusionflow.github.io/
• https://www.youtube.com/watch?v=DDq_pIfHqLs&ab_channel=Jia-BinHuang
• https://www.youtube.com/watch?v=7cMzfkWFWhI

Flow matching vs. Flow-Based Model?

Flow-based models care about exact probabilities. Flow matching cares about how to move from one distribution to another. Flow Matching bypasses the need for computing the log-determinant Jacobian or training via score-matching or log-likelihood.

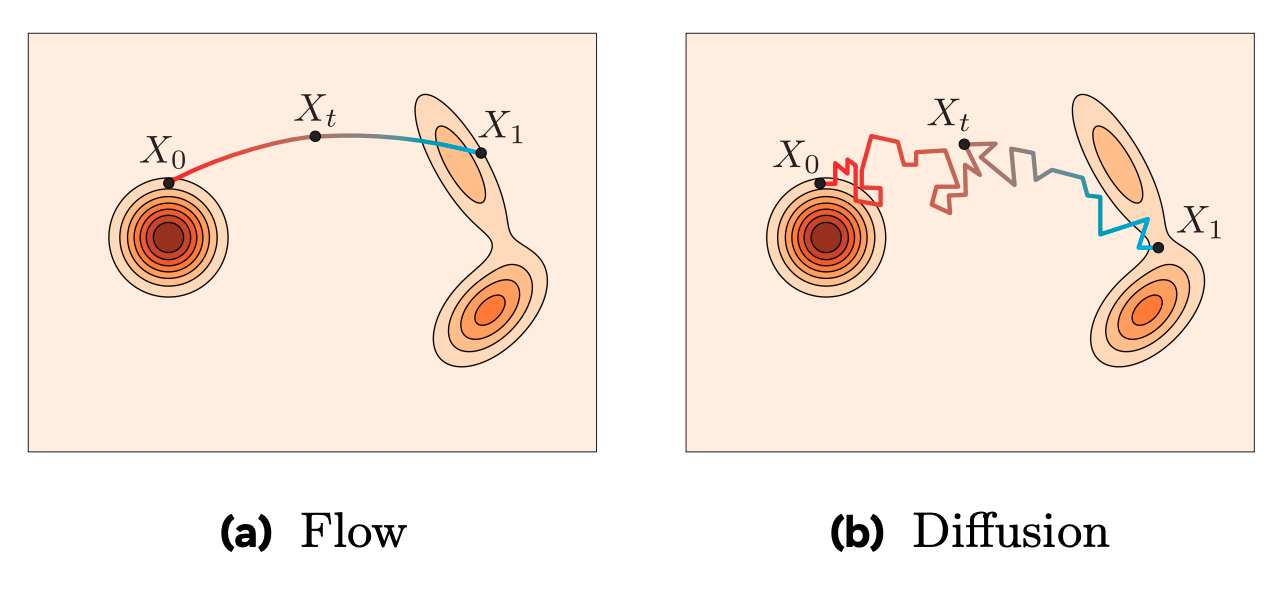
Flow matching vs. diffusion?

Image says it all.

Instead, it trains the flow function $f(x,t)$ to match a target vector field $f^{}(x,t)$ that would push a sample from the base distribution to the target distribution over time.

This makes training more stable.

Flow matching is an alternative way to train CNFs, where you learn the dynamics directly by matching flows instead of optimizing Log Likelihood.

See pi0 for equation of flow matching in context of robotics.

• Source: Mean Flows for Onestep Generative Modeling

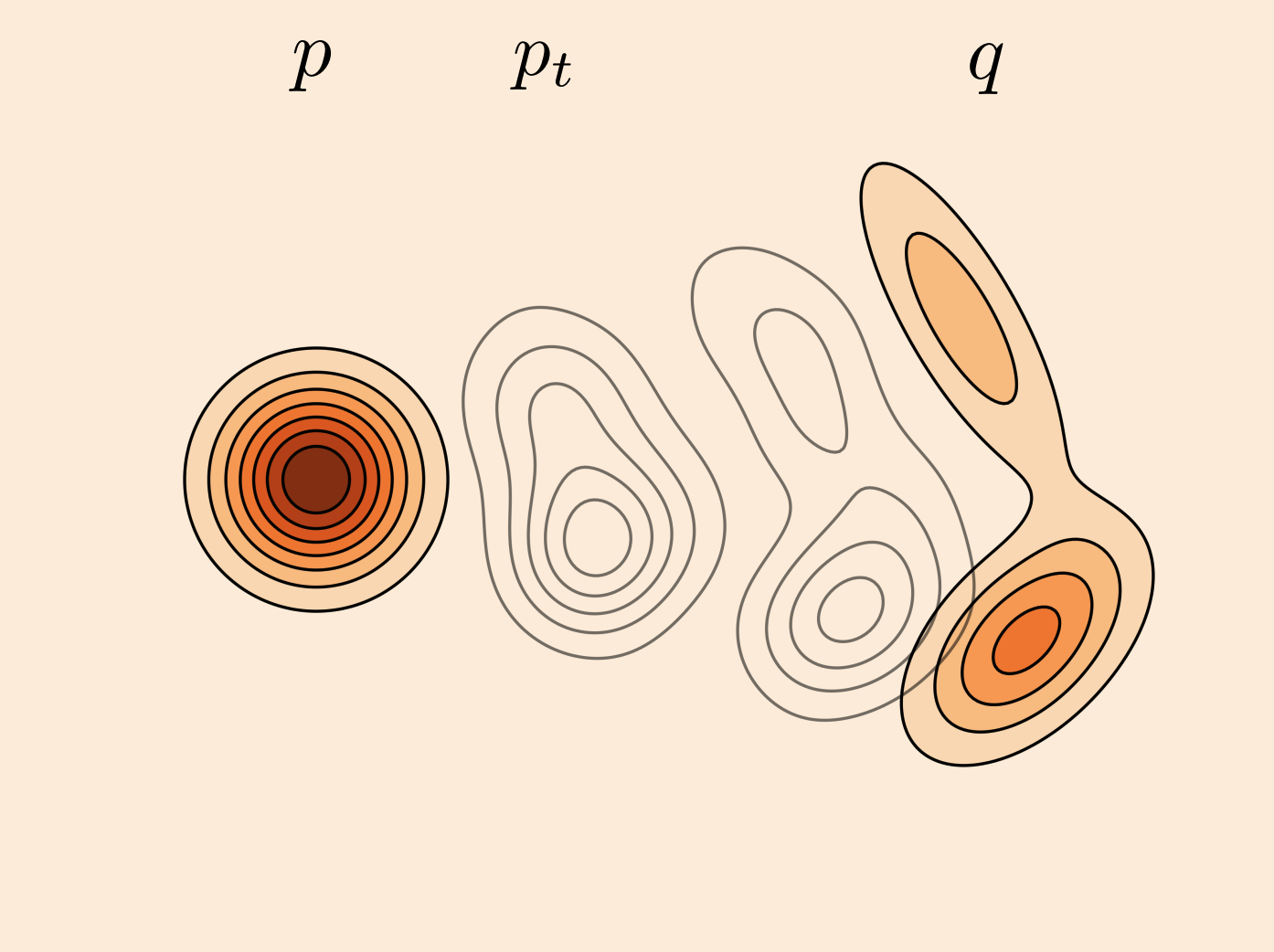
I think the above diagram is the easiest to way to visualize in 1D what’s happening. Imagine you are doing matching to map from one gaussian to the other gaussian. You end up with these curved shapes. It’s very unlikely that you go from one outlier to the other outlier (outlier to mean and mean to outlier are more common), so you’ll never learn those velocity fields.

Now, think about a multi-modal flow matching. Intuitively, you cannot do this.

• Source: One Step Diffusion via Shortcut Models

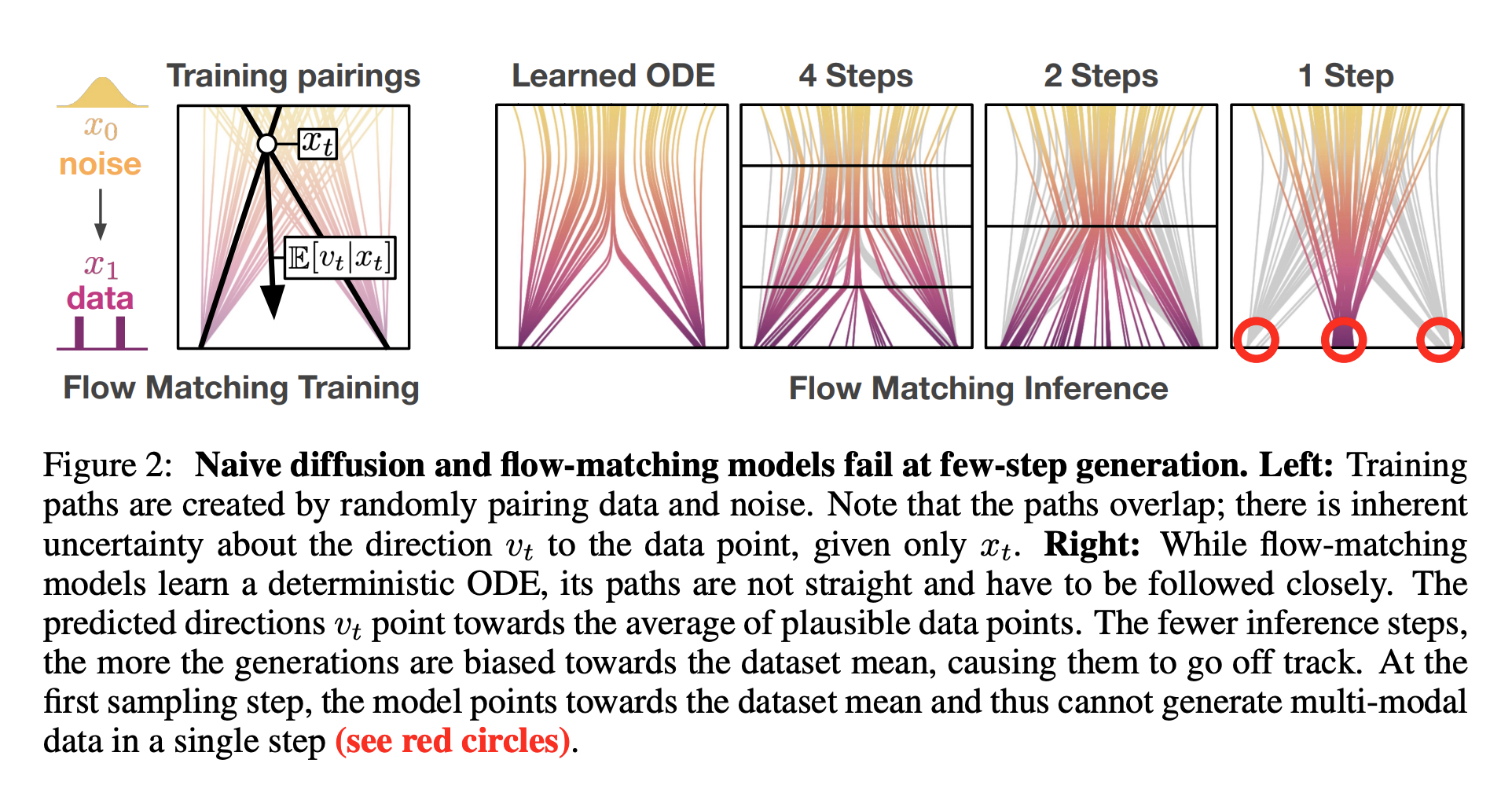
Background on flow matching

Taken from notes pi0. ChatGPT conversation: https://chatgpt.com/share/68c5b5fa-7db4-8002-9708-ef4e953533f9

The idea: we want to turn noise $ϵ\sim \mathcal{N}(0,I)$ into a data sample (here, an action $A_t$). We can describe this transformation as continuous process over time $\tau \in [0,1]$, i.e. an ODE:

$$\frac{d}{d\tau }{X}^{\tau }=v(X^{\tau },\tau ),$$

with initial condition $X^0=ϵ$ and at the end, $X^1\approx A_t$. Flow matching tries to learn this vector field $v(\cdot )$.

To train such a model, we choose reference path between $ϵ$ and $A_t$ and differentiate over it. The simplest path between $ϵ$ and $A_t$ is a straight line (i.e. straight line interpolation): $A_t^{\tau }=(1-\tau )ϵ+\tau A_t,\tau \in [0,1]$

• At $\tau =0$, you are at pure noise, and at $\tau =1$, you’re at the action

Taking the derivative with regards to $\tau$, we see that: $\frac{d}{d\tau }{A}_t^{\tau }=\frac{d}{d\tau }((1-\tau )ϵ+\tau A_t)=A_t-ϵ$

• The derivative of a straight line is a constant slope, so we just need to learn this constant!

We learn to predict this gradient (a constant) so that at inference time, we learn this mapping for any arbitrary $A_t^{\tau }$ $\frac{d}{d\tau }{A}_t^{\tau }=v_{\theta }(A_t^{\tau },o_t)=A_t-ϵ$

At inference time, we start with random noise $A_0^t\sim \mathcal{N}(0,I)$ and integrate the learned vector field from $\tau =0$ to $\tau =1$, and use forward Euler integration rule: $A_t^{\tau +\delta }=A_t^{\tau }+\delta v_{\theta }(A_t^{\tau },o_t)$

• where $\delta$ is the integration size ($\delta =0.1$ in paper)

Why is 10 steps better than 1 step?

Because at the end of the day, we are trying to learn multi-modal distributions.

• ChatGPT answer: If you take 10 smaller steps, each step only needs to be locally correct. Integration keeps pulling you back onto the line. So error doesn’t explode; it averages out

Related

• Normalizing Flow
• Transition Matching
• One Step Diffusion via Shortcut Models