Flow-Based Model

Normalizing Flow

A normalizing flow is transforms a simple distribution (generally a Unit Gaussian) into a complex, data-like distribution using a sequence of invertible and differentiable functions.

This is an idea that I saw Billy Zheng write about https://hongruizheng.com/2020/03/13/normalizing-flow.html

Resources

• https://lilianweng.github.io/posts/2018-10-13-flow-models/

Normalizing flow learns an invertible transformation $f$ between data and latent variables: $x=f(z),z=f^{-1}(x)$

• $x$ is a data sample
• $z$ is a latent variable sampled from a simple distribution

You can't just have z - z

The function $f$ in normalizing flows is perfectly invertible. In normalizing flows, we care about density estimation, not reconstruction. The loss is based on the log-likelihood of data $x$ under the model (more below).

• that would basically be an Autoencoder

We can write this in terms of probability density function (comes from the change of variables theorem in probability): $x=f(z),p(x)=p(z)\left|\det \left(\frac{\partial f^{-1}}{\partial x}\right)\right|$

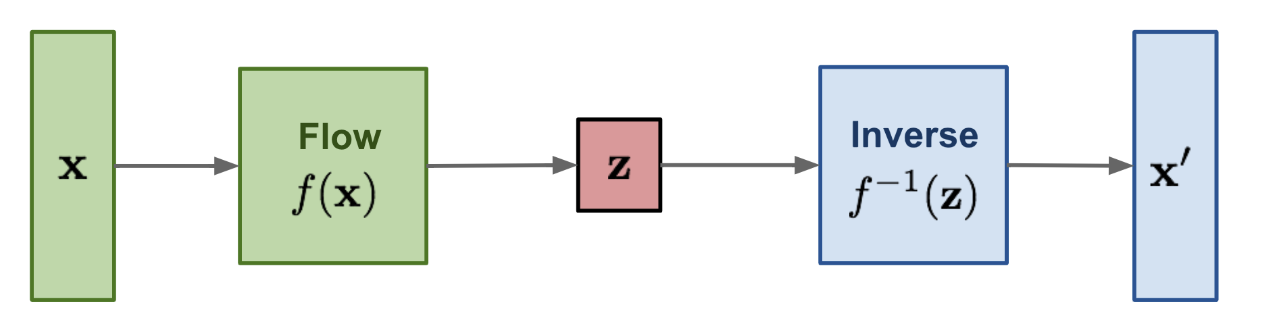
• In training, data flows from $x\to z$, use data $x$, and apply the inverse flow: $z=f^{-1}(x)$. We minimize the loss over $f^{-1}$. Compute the log-likelihood using the change-of-variable formula: $\log p_X(x)=\log p_Z(z)+\log \left|\det \left(\frac{\partial f^{-1}}{\partial x}\right)\right|$
  • Notice the magic, because below, we can then use $f$! All thanks to the fact that $f$ is invertible.
• In sampling / generation, Data flows from: $z\to x$, sample $z\sim \mathcal{N}(0,I)$ from the base distribution, and apply the forward flow: $x=f(z)$

Difference with VAE?

It’s how we formulate the loss. In VAE, the encoder and decoder are separate networks. Also:

• Normalizing flow is deterministic: No randomness is added when transforming $x\leftrightarrow z$. It’s exact, we know what happens.
• VAE is stochastic: it uses a stochastic encoder that samples $z$ from a learned distribution $q(z|x)$. It outputs a distribution.

So it seems that they both model gaussians:

• In flows, the Gaussian is transformed through exact, invertible functions to match the data.
• In VAEs, the model learns to approximate the mapping between data and latent Gaussian through separate encoder/decoder networks.

Sampling:

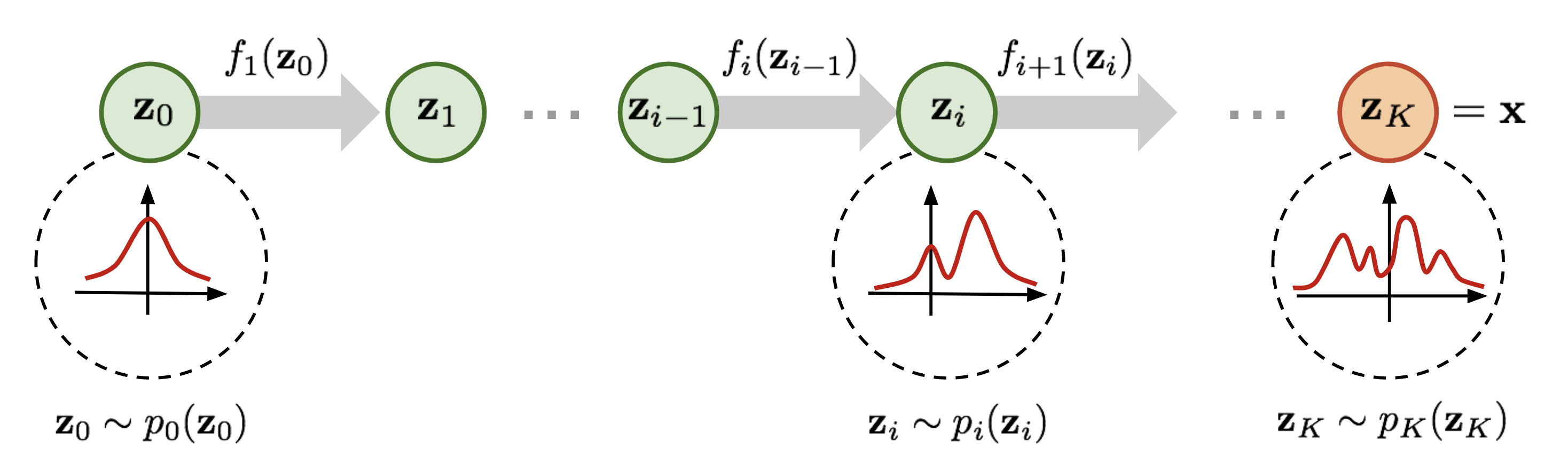We apply a chain of invertible transformations:

$$\mathbf{x}=f_K\circ f_{K-1}\circ \cdots \circ f_1({\mathbf{z}}_0)$$

• ${\mathbf{z}}_0\sim \mathcal{N}(0,I)$: latent variable sampled from a standard Gaussian
• Each $f_i$: an invertible transformation (e.g., affine coupling layer)
• Output $\mathbf{x}$: a realistic-looking data sample

What does $f$ look like? Depends on the model. They’re generally just Affine Transforms, since those are differentiable.

Forward pass:

$$\begin{array}{rl}{\mathbf{y}}_a& ={\mathbf{x}}_a\\ {\mathbf{y}}_b& ={\mathbf{x}}_b\odot \exp (s_{\theta }({\mathbf{x}}_a))+t_{\theta }({\mathbf{x}}_a)\end{array}$$

Inverse pass:

$$\begin{array}{rl}{\mathbf{x}}_a& ={\mathbf{y}}_a\\ {\mathbf{x}}_b& =({\mathbf{y}}_b-t_{\theta }({\mathbf{y}}_a))\odot \exp (-s_{\theta }({\mathbf{y}}_a))\end{array}$$

• $s_{\theta }$ and $t_{\theta }$ are neural networks (often small CNNs or MLPs).
• Same parameters are reused in both directions.

How Weight Updates Work in Flow-Based Models

Training is done via maximum likelihood estimation (MLE) using the change-of-variables formula.

Change of Variables

Given $\mathbf{x}=f(\mathbf{z})$ and $\mathbf{z}\sim \mathcal{N}(0,I)$:

$$\log p_X(\mathbf{x})=\log p_Z(f^{-1}(\mathbf{x}))+\log \left|\det \left(\frac{\partial f^{-1}}{\partial \mathbf{x}}\right)\right|$$

Rewriting using forward Jacobian:

$$\log p_X(\mathbf{x})=\log p_Z(\mathbf{z})-\log \left|\det \left(\frac{\partial f}{\partial \mathbf{z}}\right)\right|$$

The fundamental differnce

This loss uses a jacobian, it’s derived from the change of variables formula.

• We’re not just doing L = x - f(z)

Training Steps

1. Inverse pass: Given data $\mathbf{x}$, compute $\mathbf{z}=f^{-1}(\mathbf{x})$
2. Compute log-likelihood loss:

$$\mathcal{L}=-\log p_Z(\mathbf{z})+\log \left|\det \left(\frac{\partial f}{\partial \mathbf{z}}\right)\right|$$

3. Backpropagate through:

   • the inverse transformations $f^{-1}$
   • the neural nets $s_{\theta }$ and $t_{\theta }$
   • the log-determinant term (structured for easy computation in RealNVP/Glow)

4. Gradient Descent:

   • Use Adam/SGD to update parameters $\theta$ in $s_{\theta }$ and $t_{\theta }$

Normalizing flow gives you an explicit representation of density functions.

• Kernel Density Estimation

Used a lot in Generative Model.

Related

• Flow Matching