Planar Graph

Kuratowski’s Theorem

Kuratowski's Theorem (Theorem 7.6.1)

A graph is planar if and only if it does not contain an edge subdivision of $K_{3,3}$ or $K_5$ as a subgraph.

The proof for this is seen in CO342.

This theorem is used to prove that a graph is non-planar.

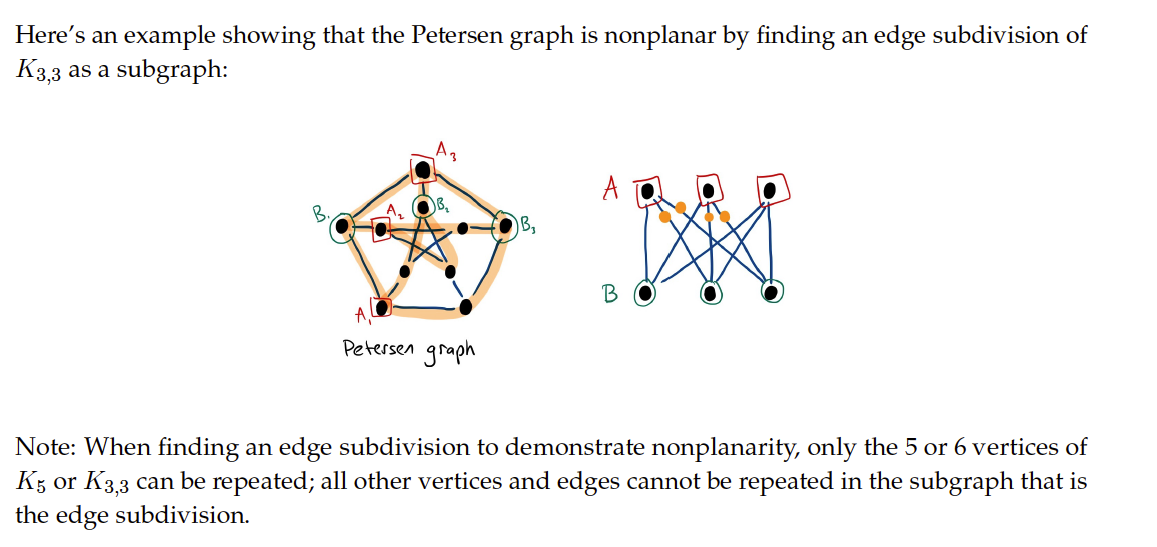
Warning

You cannot repeat edges when you try to find the edge subdivision.

To convince yourself: Else, About a planar graph that looks similar to $K_5$, with one vertex in the center. If you can repeat vertices, you would easily be able to build $K_5$, and come to a contradiction.

Tip

At first, I was really struggling, but it just comes down to 2 steps:

1. Selecting your bipartition of vertices, and alternate.
2. Then, color in your edges. It just works oftentimes