Graph Theory

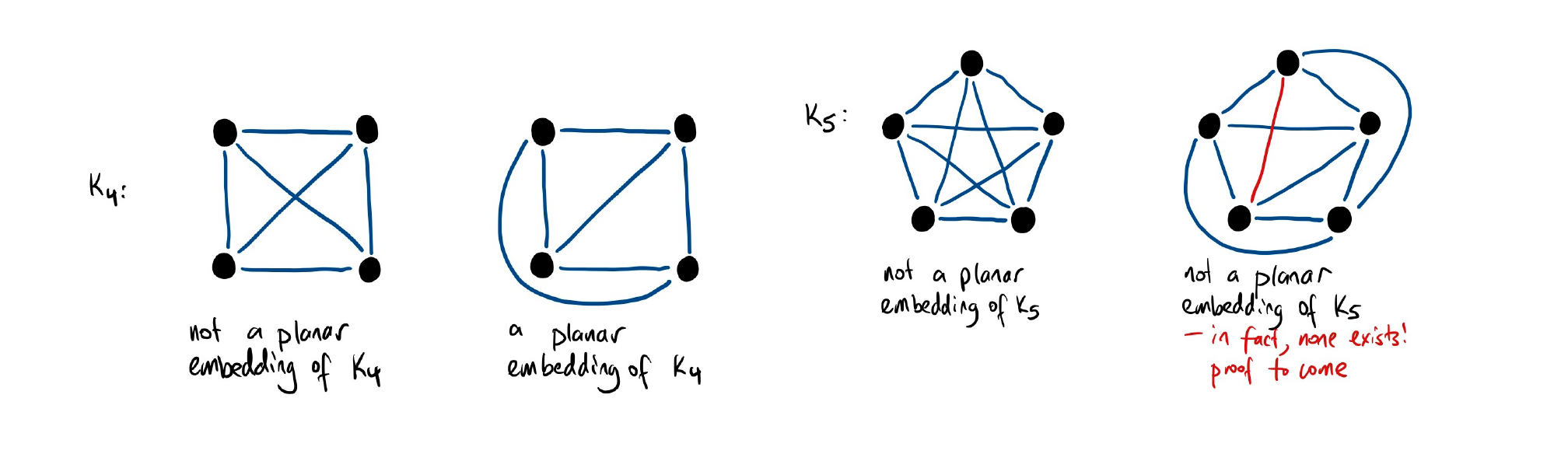
Planar Graph

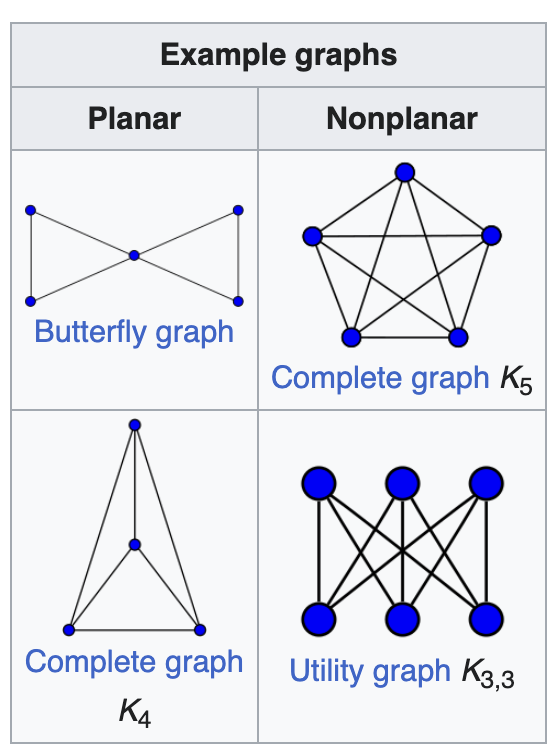
A planar graph is a graph that can be drawn without edges crossing (i.e. edges intersect only at their endpoints).

Why are planar graphs important?

Planar graphs are important because they have various practical applications in computer science, networking, and circuit design, and they serve as a foundation for studying more complex graph structures.

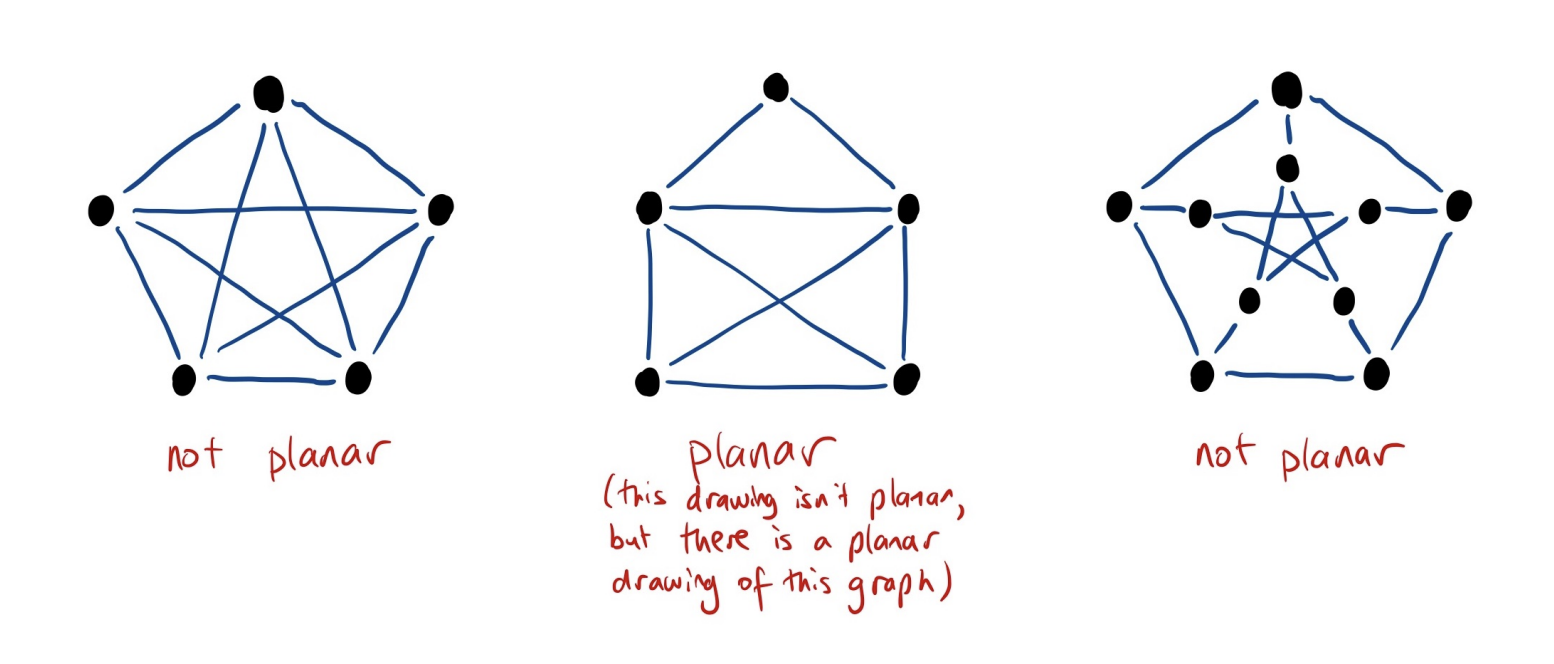
• A graph is planar if and only if each of its components is planar
• A graph is planar $⟺$ each of its components is planar

Definitions

Definition 1

A planar embedding of a graph $G$ is a drawing of the graph in the plane so that its edges intersect only at their ends (i.e., edges do not cross), and no two vertices occupy the same point. A graph that has a planar embedding is called planar.

Definition 2

A face of a planar embedding is a connected region of the plane.

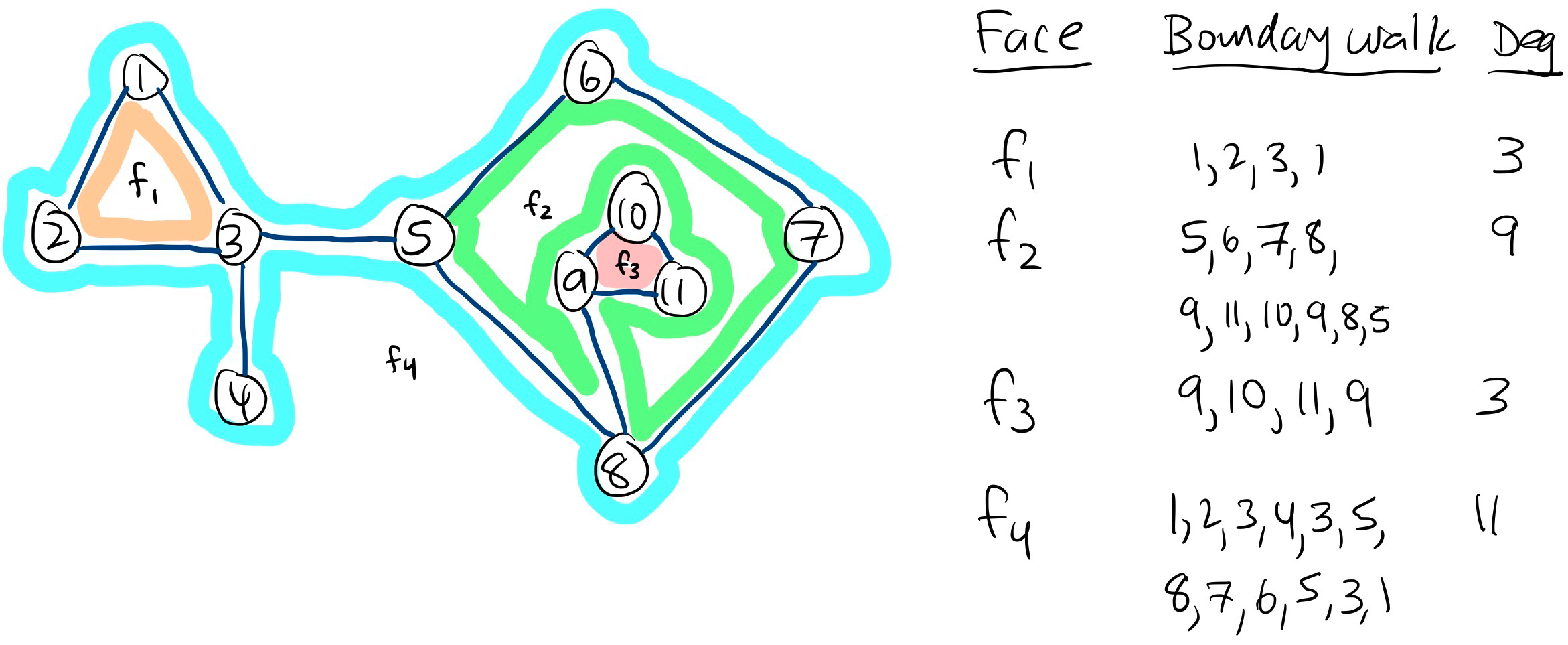
Definition 3

The boundary of a face is the subgraph formed from all vertices and edges that touch the face. Two faces are adjacent if their boundaries have at least one edge in common

Definition 4

For a planar embedding of a connected graph, the boundary walk of a face is a closed walk once around the perimeter of the face boundary. The degree of a face $f$ is the length of the boundary walk of the face, denoted $\mathrm{deg}(f)$.

What is a face? Asked ChatGPT

The face of a planar embedding is a region of the plane that is bounded by edges of the graph. In simpler terms, you can think of the faces as the enclosed areas between the edges of a graph drawn on a plane.

Definition 1

An edge subdivision of $G$ is obtained by replacing each edge of $G$ with a new path of length at least $1$.

Theorems and Lemmas

Faceshaking Lemma ( Handshaking Lemma for Faces), Theorem 7.12

Let $G$ be a connected planar graph with a planar embedding, where $F$ is the set of all faces. Then

${\sum }_{v\in F}deg(v)=2|E(G)|$

Proof. Each edge has 2 sides, and each side contributes to 1 to a boundary walk, so the edge contributes 2 to the sum of degrees.

Lemma 1

In a planar embedding, an edge $e$ is a bridge if and only if the two sides of $e$ are in the same face.

Jordan Curve Theorem

Every planar embedding of a cycle separates the plane into two parts, one on the inside and one on the outside.

Euler's Formula (Theorem 7.2.1)

Let $G$ be a Connected Graph with $n$ vertices and $m$ edges. Consider a planar embedding of $G$ with $f$ faces. Then $n-m+f=2$.

Proving planar / non-planar graphs:

• Proving that a graph is planar is easy: draw a planar embedding.
• Proving that a graph is nonplanar is harder: a single drawing is not sufficient.

One way to prove nonplanarity: show that there are “too many” edges.

Lemma 7.5.2

Let $G$ be a planar embedding with $n$ vertices and $m$ edges. If there is a planar embedding of $G$ where every face has degree at least $d\ge 3$, then $m\le \frac{d(n-2)}{d-2}$

Theorem 7.5.3

Let $G$ be a planar graph with $n\ge 3$ vertices and $m$ edges. Then $m\le 3n-6$.

• Can prove a graph is nonplanar, but cannot be used to prove that a graph is planar (there are cases where $m\le 3n-6$ but the graph is nonplanar), it’s not a IFF relationship

Lemma 7.5.1

If $G$ contains a cycle, then in any planar embedding of $G$, every face boundary contains a cycle.

Corollary 7.5.4

$K_5$ is not planar.

Theorem 7.5.6

Let $G$ be a bipartite planar graph with $n\ge 3$ vertices and $m$ edges. Then $m\le 2n-4$.

• same idea as theorem 7.5.3, cannot be used to prove bipartite planar graph

Corollary 7.5.7

$K_{3,3}$ is not planar.

Fact

A graph is planar if and only if any edge subdivision of the graph is planar.

From this we can immediately conclude:

Corollary 1

If $G$ contains an edge subdivision of $K_{3,3}$ or $K_5$ as a subgraph, then $G$ is not planar.

Example of using this as a proof:

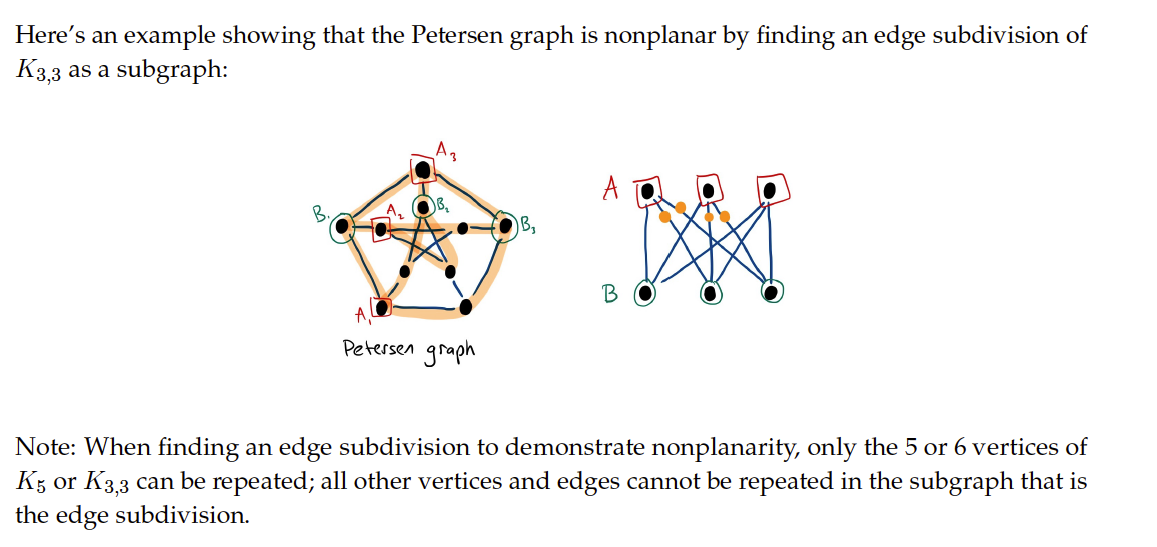
Kuratowski's Theorem (Theorem 7.6.1)

A graph is planar if and only if it does not contain an edge subdivision of $K_{3,3}$ or $K_5$ as a subgraph.

So now we have a complete way of demonstrating planarity or nonplanarity of a graph:

• Can show a graph is planar by drawing a planar embedding
• Can show a graph is nonplanar by finding an edge subdivision of $K_{3,3}$ or $K_5$ as a subgraph (Kuratowski Theorem)

Corollary 7.5.5

Every planar graph has a vertex of degree at most $5$.

Related

• Graph Colouring