Lie Algebra

They are introducing this in the SLAM book, but I have no idea what this concept is about??

A major motivation for using Lie algebra is to do optimization.

So I think the idea is that when you do certain operations with matrices, like exponentials, and remember how we like to work in different representations, like Rotation Matrix vs. Axis-Angle Representation, so how do we know that these operations hold?

• Think about taking derivatives. Does it just “work”? Need lie algebra to robustly prove this.

The reader must understand the content of this lecture, which is the basis for solving many subsequent problems, especially the pose estimation part.

For a set that only has one “well-defined operations”, we call it a group.

You will definitely need to understand this to be better at doing optimization.

Group

A group is an algebraic structure of one set plus one operator. We denote the set as $A$ and the operation as $\cdot$, then the group can be denoted as $G=(A,\cdot )$. We say $G$ is a group if the operation satisfies the following conditions:

1. Closure : $\forall a_1,a_2\in A,a_1\cdot a_2\in A$
2. Combination $\forall a_1,a_2,a_3\in A,(a_1\cdot a_2)\cdot a_3=a_1\cdot (a_2\cdot a_3)$
3. Unit element $\exists a_0\in A,s.t.\forall a\in A,a_0\cdot a=a\cdot a_0=a$
4. Inverse element: $\forall a\in A,\exists a^{-1}\in A,sta\cdot a^{-1}=a_0$

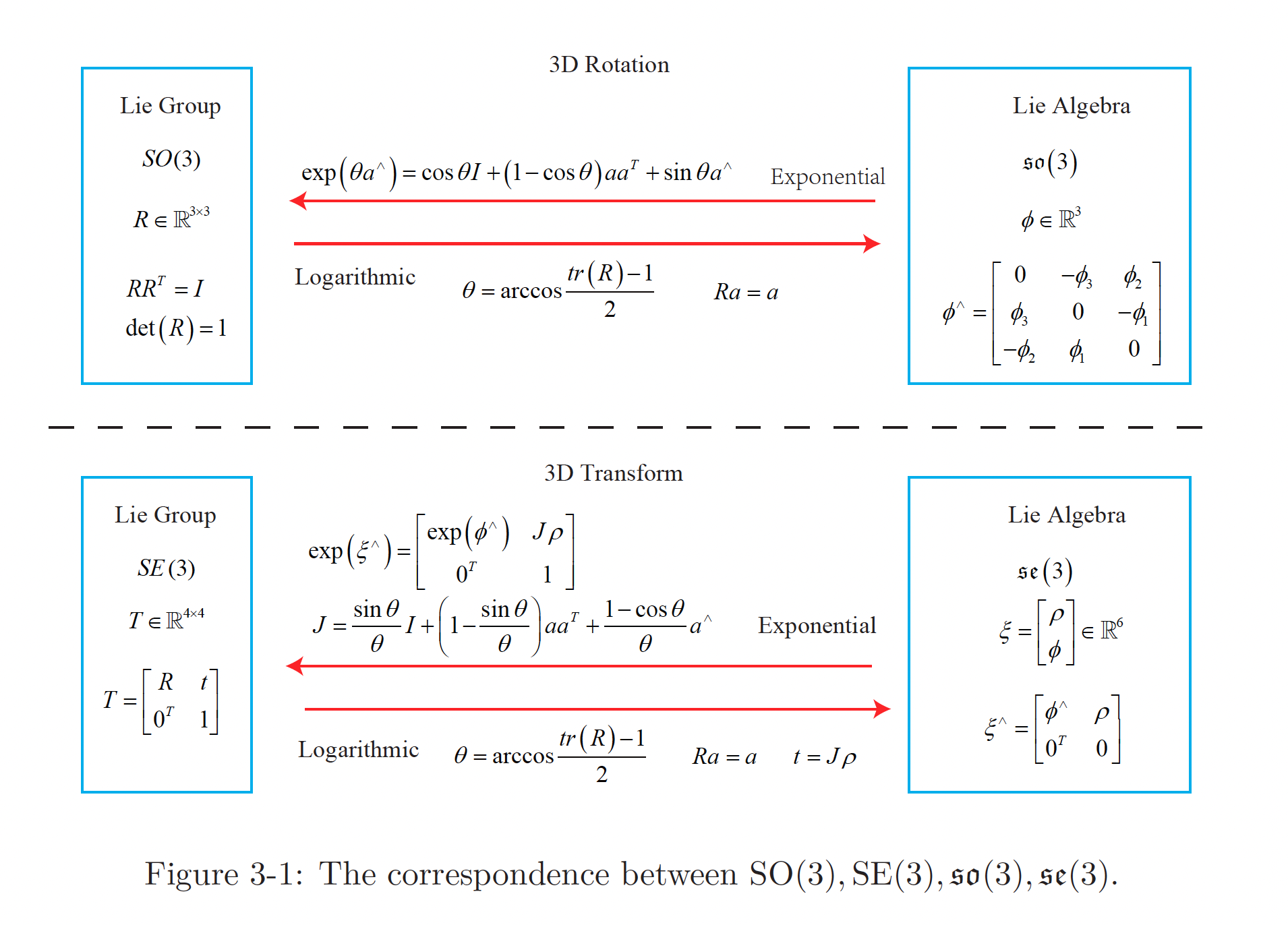
Lie algebra describes the local structure of the Lie group around its origin point, or in other words, is the tangent space. The general definition of Lie algebra is listed as follows:

Lie Algebra

A Lie algebra consists of a set $\mathbb{V}$, a scalar field $\mathbb{F}$, and a binary operation $[,]$. If they satisfy the following properties, then $(\mathbb{V},\mathbb{F},[,])$ is a Lie algebra, denoted as $\mathfrak{g}$.

$\text{1. Closure}:\forall \mathbf{X},\mathbf{Y}\in \mathbb{V};[\mathbf{X},\mathbf{Y}]\in \mathbb{V}$ $\text{2. Bilinear composition}:\forall \mathbf{X},\mathbf{Y},\mathbf{Z}\in \mathbb{V};a,b\in \mathbb{F},\text{ we have}$ $[a\mathbf{X}+b\mathbf{Y},\mathbf{Z}]=a[\mathbf{X},\mathbf{Z}]+b[\mathbf{Y},\mathbf{Z}],[\mathbf{Z},a\mathbf{X}+b\mathbf{Y}]=a[\mathbf{Z},\mathbf{X}]+b[\mathbf{Z},\mathbf{Y}]$ $\text{3. Reflexive}:\forall \mathbf{X}\in \mathbb{V};[\mathbf{X},\mathbf{X}]=0$ $\text{4. Jacobi identity}:\forall \mathbf{X},\mathbf{Y},\mathbf{Z}\in \mathbb{V};[\mathbf{X},[\mathbf{Y},\mathbf{Z}]]+[\mathbf{Z},[\mathbf{X},\mathbf{Y}]]+[\mathbf{Y},[\mathbf{Z},\mathbf{X}]]=0$

The binary operations $[,]$ are called Lie brackets. At first glance, we require a lot of properties about the Lie bracket. Compared to the simpler binary operations in the group, the Lie bracket expresses the difference between the two elements. It does not require a combination law but requires the element and itself to be zero after the brackets. For example, the cross product $\times$ defined on the 3D vector ${\mathbb{R}}^3$ is a kind of Lie bracket, so $\mathfrak{g}=({\mathbb{R}}^3,\mathbb{R},\times )$ constitutes a Lie algebra.

Readers can try to substitute the cross product into the four properties to verify the above conclusion.