Spatial Algebra

Axis-Angle Representation (Rotation Vector)

First introduction here through Steven M. Lavalle VR series. Read more into the modern robotics book, chapter 3.

Axis-Angle Representation are implemented with rotation vectors. This vector is parallel with the axis of rotation, and the length is equal to the angle of rotation.

For a rotation axis with unit-length vector $\mathbf{n}$ and the angle $\theta$, then the rotation vector is represented by $\theta \mathbf{n}$

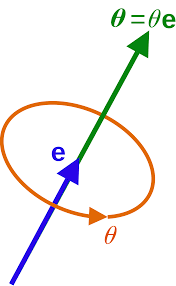
Euler's Rotation Theorem

All 3D rotations have an axis-angle representation.

At first, I thought these were the same as Euler Angles.

But NO! With Euler Angles, we have 3 rotation angles expressed relative to 3 fixed axes $x$, $y$, and $z$-axis (pitch, roll and yaw).

On the other hand, angle-axis representation, expresses a rotation as a single rotation by an angle around a specific axis. Thus, only a 3D vector here is needed to describe the rotation.

Because of Euler’s Rotation Theorem, we know that the 3 rotations can simply collapse to 1 rotation around a given axis: any sequence of rotations in 3D space is equivalent to a pure rotation about a single fixed axis.

Rotation Vector to Rotation Matrix

Rodrigues' Formula

The conversion from rotation vector to rotation matrix is shown by Rodrigues’ formula. The result of the conversion is the follow

$R=\cos \theta \mathbf{I}+(1-cos\theta ){\mathbf{nn}}^T+\sin \theta {\mathbf{n}}^{\wedge }$ where

• $\mathbf{R}$ is the rotation matrix
• the rotation axis has unit length vector $\mathbf{n}$ and angle $\theta$
• ${}^{\wedge }$ is the Skew-symmetric operator

Since the rotation axis does not change after the rotation, we have $\mathbf{Rn}=\mathbf{n}$ Therefore, the axis $\mathbf{n}$ is the eigenvector corresponding to the matrix $\mathbf{R}$’s Eigenvalue 1.

I think you can learn more about the formalization with Lie Algebra.

Usage in Eigen

// AngleAxisd rotation_vector(angle, vector);
AngleAxisd rotation_vector(M_PI/4, Vector3d(0,0,1));

Related

• Euler Angle
• Rotation Matrix
• Quaternion