Natural Deduction

Natural deduction is a proof theory for showing the validity of an argument in propositional logic.

Natural deduction is a collection of rules, called inference rules, each of which allows us to infer new formulas from given formulas.

Natural deduction is a form of forward proof. Starting from the premises, we use the inference rules to deduce new formulas that logically follow from the premises. Using the formulas we have proven and the premises, we use the rules to deduce more formulas. We continue this process until we have deduced the conclusion. So we use Logical Implication. $P_1,P_2,\dots ,P_n⊢Q$

Natural Deduction Rules

For Predicate Logic

The names:

• and_i = and-inclusion
• and_e = and-elimination
• etc.

Some Strategies:

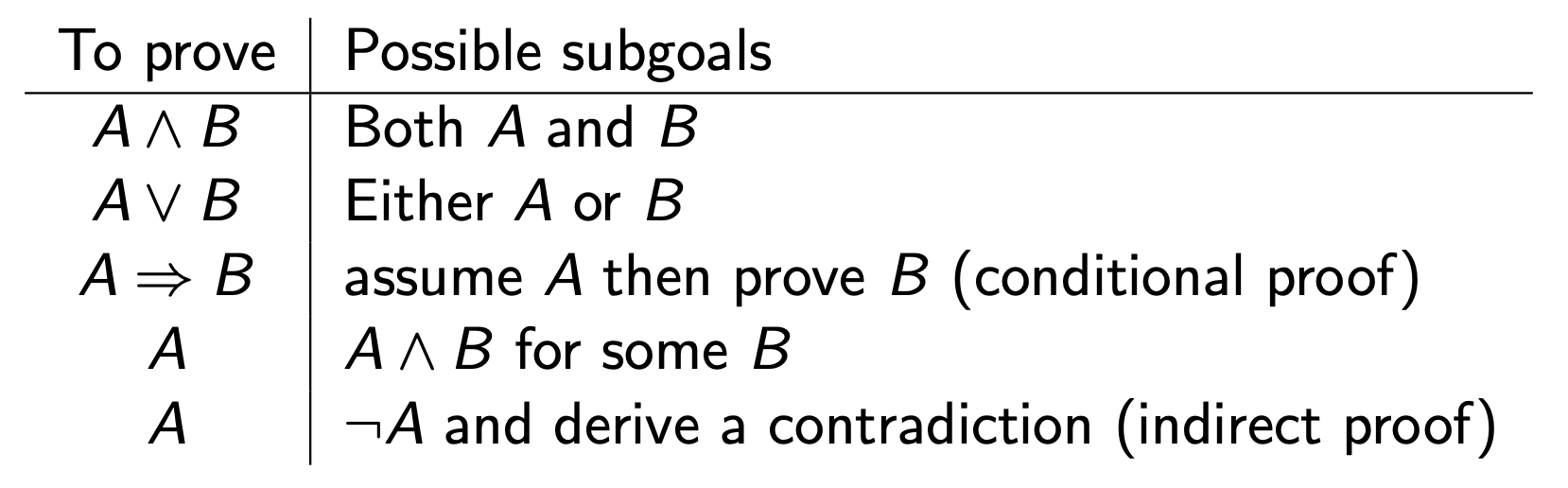
Any natural deduction proof can be Transformational Proof. But be careful, this is in transformational proof $((b⟹c)\wedge (b⟹\neg c))⟹\neg b<->true$

NOT THE SAME AS $((b⟹c)\wedge (b⟹\neg c)<->\neg b$ Because the above is stronger. We need to use the first interpretation.

If you are still confused, see Logical Implication

Examples

b |- a => b um this is wrong

1) b premise
2) assume a {
	3) disprove !b { 
		35)  false # I need to double check this
	}
	4) b by raa on 3-35
	}
 }
 a => b by imp_i on 2-4

Some more proofs

1) a premise
2) !b <=> a premise
3) c | b premise
4) c => b premise
5) !b by iff_mp on 1,2
6) case c {
	7) !c by imp_e on 4,5
	8) false by not_e on 6,7
}
9) case b {
10) false by not_e on 5,9
}
11) false by cases on 3,6-8,9-10

Prove this: |- (p | !p)

1) disprove !(p|!p) {
	2) disprove p {
		3) p | !p by or_i on 2
		4) false by not_e on 1,3
		}
	5) !p by raa on 2-4
	6) p | !p by or_i on 5
	7) false by not_e on 1,6
}
8) p | !p by raa on 1-7

Proving De Morgan’s Laws (DML) through De Morgan’s Laws (DML) through Natural Deduction: $(\neg a\vee \neg b)⊢\neg (a\wedge b)$

1) !a | !b premise
2) disproof (a & b) {
	3) a by and_e on 2
	4) b by and_e on 2
	5) !!a by not_not_i on 3
	6) !b by or_e on 1,5
	7) false by not_e on 4,6
}
8) !(a & b) by raa on 2-7

$\neg (a\vee b)⊢(\neg a\wedge \neg b)$

1) !(a|b) premise
2) disprove a {
	3) a|b by or_i on 2
	4) false by not_e on 1,3
}
5) !a by raa on 2-4
6) disprove b {
	7) a|b by or_i on 6
	8) false by not_e on 1,7
}
9) !b by raa on 6-8
10) !a & !b by and_i on 5,9

$b⟹c⊢(\neg b\vee c)$

1) b => c premise
2) b | !b by lem
3) case b {
4) c by imp_e on 1,3
5) !b | c by or_i on 4
}
6) case !b {
7) !b | c by or_i on 6
}
8) !b | c by cases on 2, 3-5, 6-7