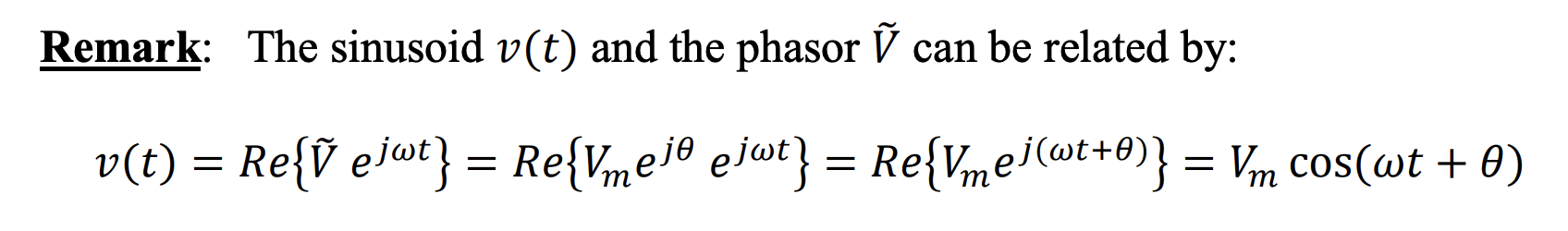Phasor

Phasor = “Phase vector”

Given the sinusoid $v(t)=V_m\cos (\omega t+\theta )$, its phasor is a complex number defined by $\tilde{V}=V_m{e}^{j\theta }=V_m\angle \theta$

IMPORTANT: the sinusoid must be written as a $\cos$ function for this relationship.

Example of Conversion

If the voltage is given by $v(t)=3\cos (wt+30°)$, its phasor-domain is given by $\tilde{V}=3\angle 30°$

What happens to the frequency \omega?

Notice that the phasor does not represent the angular frequency $\omega$. Thus, every phasor is associated with a specific frequency.

$\to$ When several phasors are manipulated together, they must be associated with the same frequency.

Why Phasors?

The phasor is basically a polar form of a Complex Number used for AC Circuit Analysis.

Instead of working in the time-domain, with a Sinusoidal function (sin functions), we can just imaginary numbers in the phasor-domain to make the algebra doable.

• Helps visualize current and voltage relationships, see Phasor Diagram

Phasor - Rectangular - Sinusoidal

Make sure to understand the relationship between all three of them.

All three forms are equivalent!! But note that that the phasor and rectangular are associated with the specific frequency.

Phasor	Rectangular	Sinusoidal
$V_m\angle \theta$	$V_m(\cos \theta +j\sin \theta )$	$V_m\sin (wt+\theta )$

Some thoughts that might be wrong for me to consolidate my knowledge

#gap-in-knowledge

I dont know why phasors works…i.e. why the mapping from time-domain to phasor domain works?

I think the way to think about it is why are both of them logically equivalent? We invented this concept. They are not exactly quivalent to each other, (we lose information on $\omega$ as well as $t$ in the phasor!), but this technique helps us solve equations more easily, as we don’t always need $t$ and $\omega$.

See here for animation!

Also, check out the textbook to read more upon it!

Related

• Phasor Diagram
• AC Circuit Analysis