Complex Number

Three ways to represent a complex number.

• Standard Form
• Polar Form
• Complex Exponential Form

Standard Form

Definition: A complex number in standard form is an expression of the form $x+yj$ where $x,y\in \mathbb{R}$ and $j$ satisfies $j^2=-1$. The set of all complex numbers is denoted by $\mathbb{C}=\{x+yj\mid x,y\in \mathbb{R}\}$

Note

Note that I learned to use $j$ rather than $i$ since that letter is used in the modelling of electric networks.

Danger

$i$ is NOT equal to $\sqrt{-1}$. If it were, then $-1=i^2=i\cdot i=\sqrt{-1}\cdot \sqrt{-1}=\sqrt{-1\cdot -1}=\sqrt{1}=1$

Real and Imaginary Parts

Let $z=x+yj\in \mathbb{C}$ with $x,y\in \mathbb{R}$. $x=\text{Re}(z)$ $y=\text{Im}(z)$

Inverse of Complex Number

For $z\in \mathbb{C}$, $z=x+yj$, $z^{-1}$ exists if and only if $z\ne 0$. Besides, when it exists, $z^{-1}=\frac{x}{x^2+y^2}-i\frac{y}{x^2+y^2}$

Conjugate

The complex conjugate of $z=x+yj$ with $x,y\in \mathbb{R}$ is $\overline{z}=x-yj$

Properties of Conjugates. Let $z,w\in \mathbb{C}$ with $z=x+yj$ where $x,y\in \mathbb{R}$. Then $\overline{\stackrel{ˉ}{z}}=z$ $z\in \mathbb{R}⟺\bar{z}=z$ $z\text{is purely imaginary}⟺\bar{z}=-z$ $\overline{z+w}=\overline{z}+\overline{w}$ $\overline{zw}=\overline{z}\overline{w}$ $\overline{z^k}={\overline{z}}^k\text{for}k\in \mathbb{Z},k\ge 0,(k\ne 0\text{if}z=0)$ $\overline{(\frac{z}{w})}=\frac{\overline{z}}{\overline{w}}$ $z+\bar{z}=2x=2\text{Re}(z)$ $z-\bar{z}=2yj=2j\text{Im}(z)$ $z\bar{z}=x^2+y^2$

Modulus

The modulus of $z=x+yj$ with $x,y\in \mathbb{R}$ is the nonnegative real number $|z|=\sqrt{x^2+y^2}$

Modulus

The modulus is basically the absolute value if we are dealing with real numbers, and this is actually where the modulus comes from.

Properties of Modulus. Let $z,w\in \mathbb{C}$. Then $|z|=0⟺z=0$ $|\bar{z}|=|z|$ $z\bar{z}=|z{|}^2$ $|zw|=|z||w|$ $|\frac{z}{w}|=\frac{|z|}{|w|}\text{provided}w\ne 0$ $|z+w|\le |z|+|w|\text{which is known as the Triangle Inequality}$

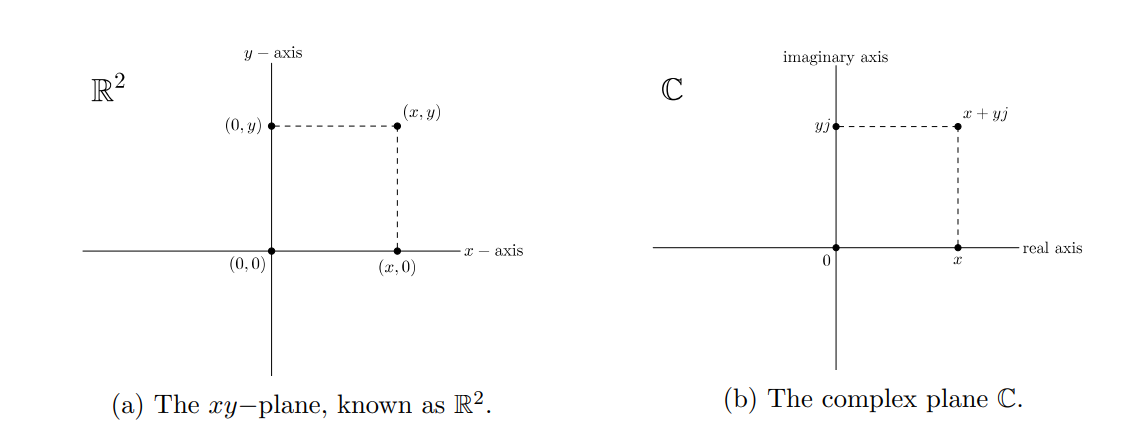
Geometry of $\mathbb{C}$ Graphically

Polar Form

There is another way we can represent imaginary numbers, which will be super useful for complex multiplication and division.

We invent this plot, where the x-axis are the Real numbers and y-axis are the imaginary numbers. 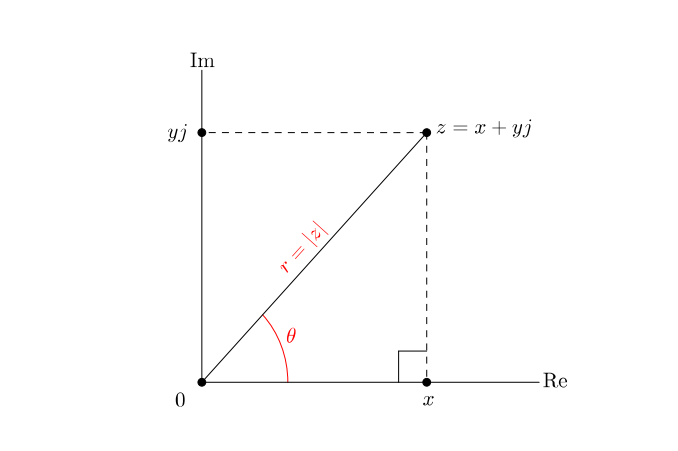We see from the above image that $\cos \theta =\frac{x}{r}\sin \theta =\frac{y}{r}$

The polar form of a complex number $z\ne 0$ is given by $z=r(\cos \theta +j\sin \theta )=r\angle \theta$ where $r=|z|$ and $\theta$ is an argument of $z$.

Polar Form: Use z=r\angle\theta

When I first learned polar form in MATH115, we always wrote it as $z=r(\cos \theta +j\sin \theta )$, but this is super long. Instead, just use $z=r\angle \theta$ which provides the same amount of information in a very concise way.

Exercise: Write $z=1+\sqrt{3}j$ in polar form.

$r=|1+\sqrt{3}j|=\sqrt{1^2+{\sqrt{3}}^2}=2$ $z=2(\frac{1}{2}+\frac{\sqrt{3}}{2}j)$

Since we have $\cos \theta =\frac{1}{2}$ and $\sin \theta =\frac{\sqrt{3}}{2}$, we know that $\theta =\frac{\pi }{3}$ Answer: $z=2(\cos \frac{\pi }{3}+j\sin \frac{\pi }{3})$

Polar Multiplication and Division

Multiplication $z_1{z}_2=r_1{r}_2\angle ({\theta }_1+{\theta }_2)$ Division $\frac{z_1}{z_2}=(\frac{r_1}{r_2})\angle ({\theta }_1-{\theta }_2)$

The MATH115 notation… $z_1{z}_2=r_1{r}_2(\cos ({\theta }_1+{\theta }_2)+j\sin ({\theta }_1+{\theta }_2))$ $\frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos ({\theta }_1-{\theta }_2)+j\sin ({\theta }_1-{\theta }_2))$

Powers of Complex Numbers

de Moivre’s Theorem. If $z=r(\cos (n\theta )+j\sin (n\theta ))\ne 0$, then $z^n=r^n(\cos (n\theta )+j\sin (n\theta ))$ for any $n\in \mathbb{Z}$.

Complex nth Roots

Let $z=r(\cos \theta =j\sin \theta )$ be nonzero, and let n be a positive integer. Then the n distinct nth roots of z are given by $w_k=r^{1/n}(\cos (\frac{\theta +2k\pi }{n})+j\sin (\frac{\theta +2k\pi }{n}))$ for $k=0,1,\dots ,n-1$

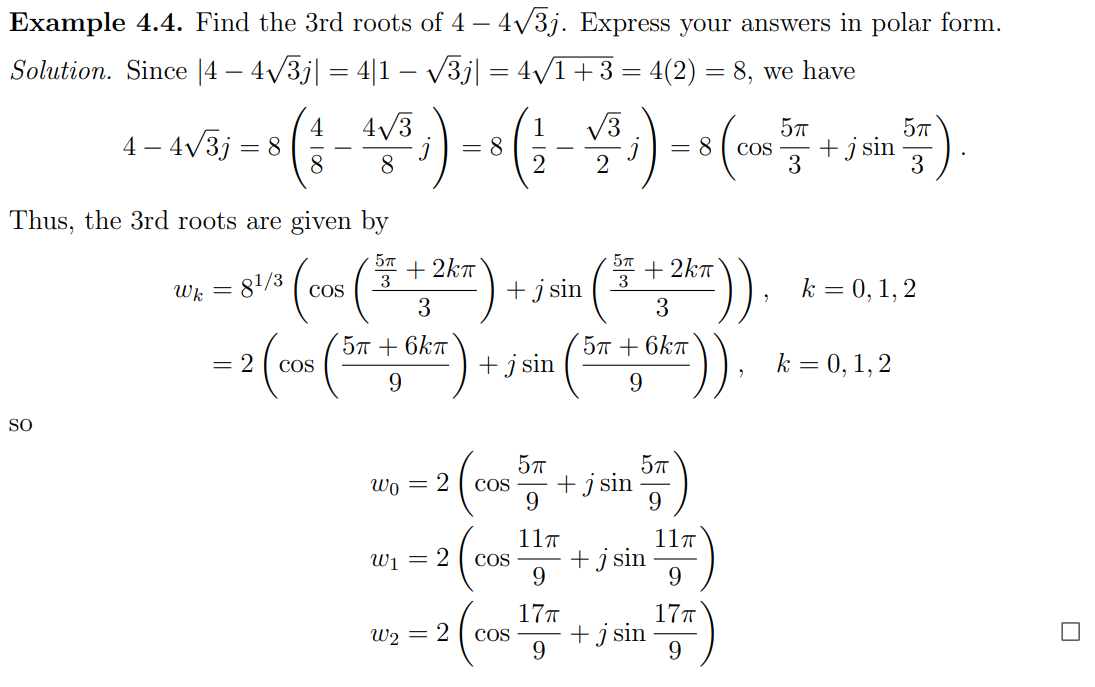
Complex Exponential Form

Why is this form useful?

Exponential form is really cool, because we can actually start relating exponentials with sins and angles!

Derived from Euler Formula, the complex exponential form of $z$ is given by $z=r{e}^{j\theta }$

Complex Polynomials

Theorem 5.2. Let $p(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdot \cdot \cdot +a_{1}x+a_0$ be a real polynomial. If $z\in \mathbb{C}$ is a root of $p(x)$, then so too is $\bar{z}$.