Quadtree

A quadtree is a tree data structure in which each internal node has exactly four children.

Formalization

We have $n$ points $S = {(x_{0}, y_{0}), (x_{1}, y_{1}),\cdot\cdot\cdot, (x_{n - 1}, y_{n - 1})}$ in the plane. We need a bounding box $R = [0, 2^{k}) \times [0, 2^{k})$ , i.e. a square containing all points.

Find the smallest $k$ such that the max $x$ and $y$ values in $S$ are $< 2^{k}$ .
Variation: Pick left coordinate based on min value, such that size is a power of 2

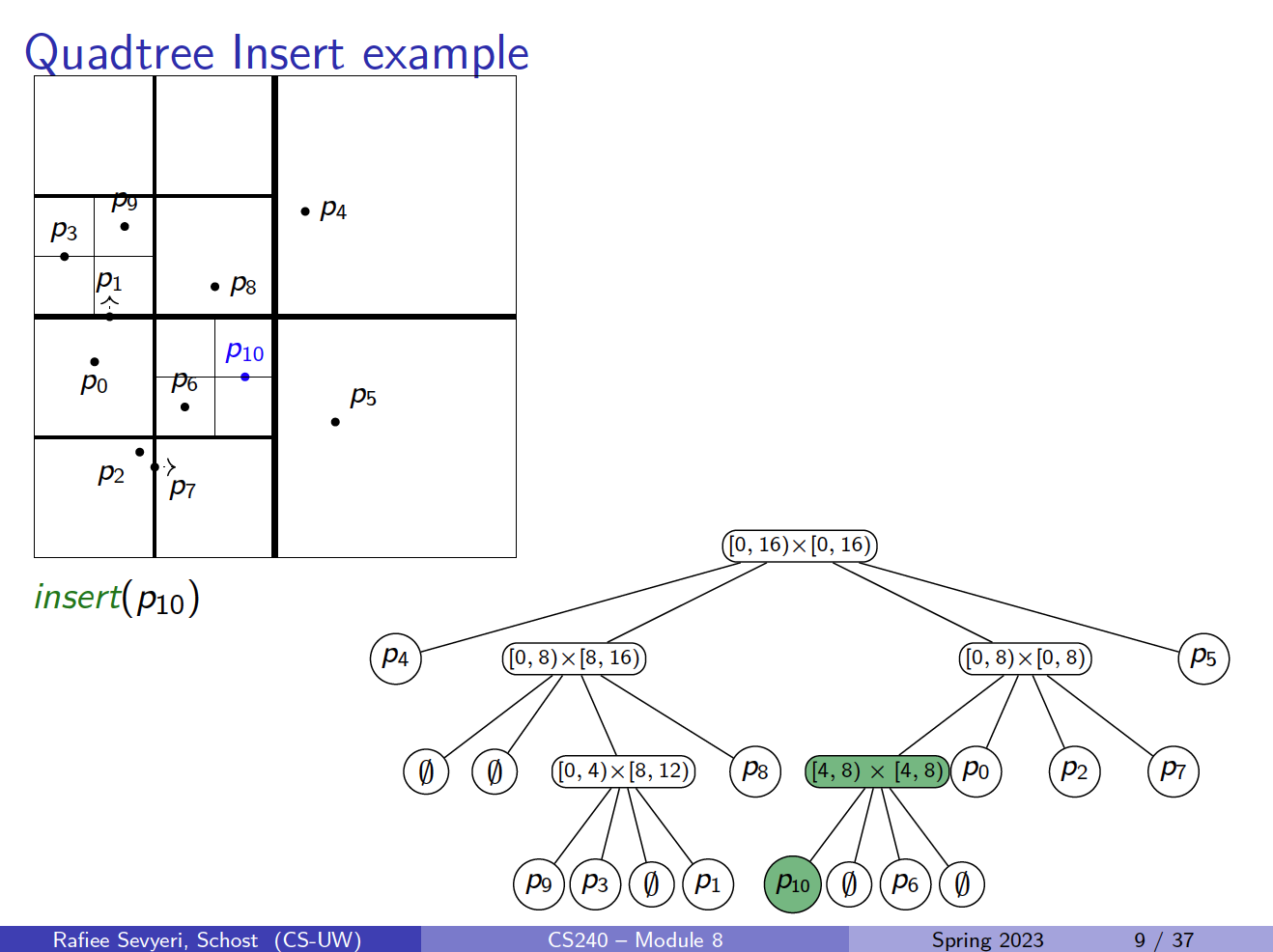
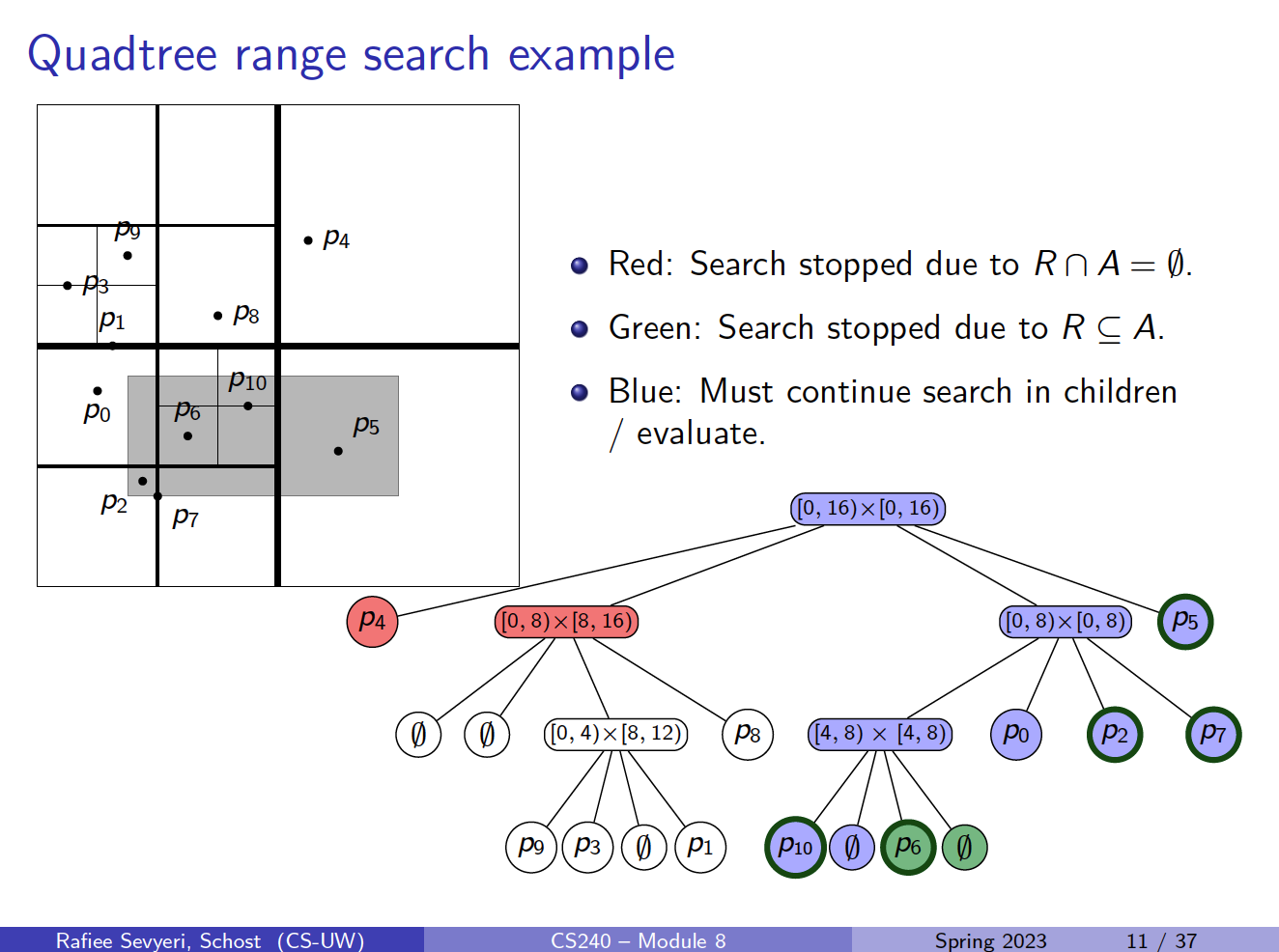
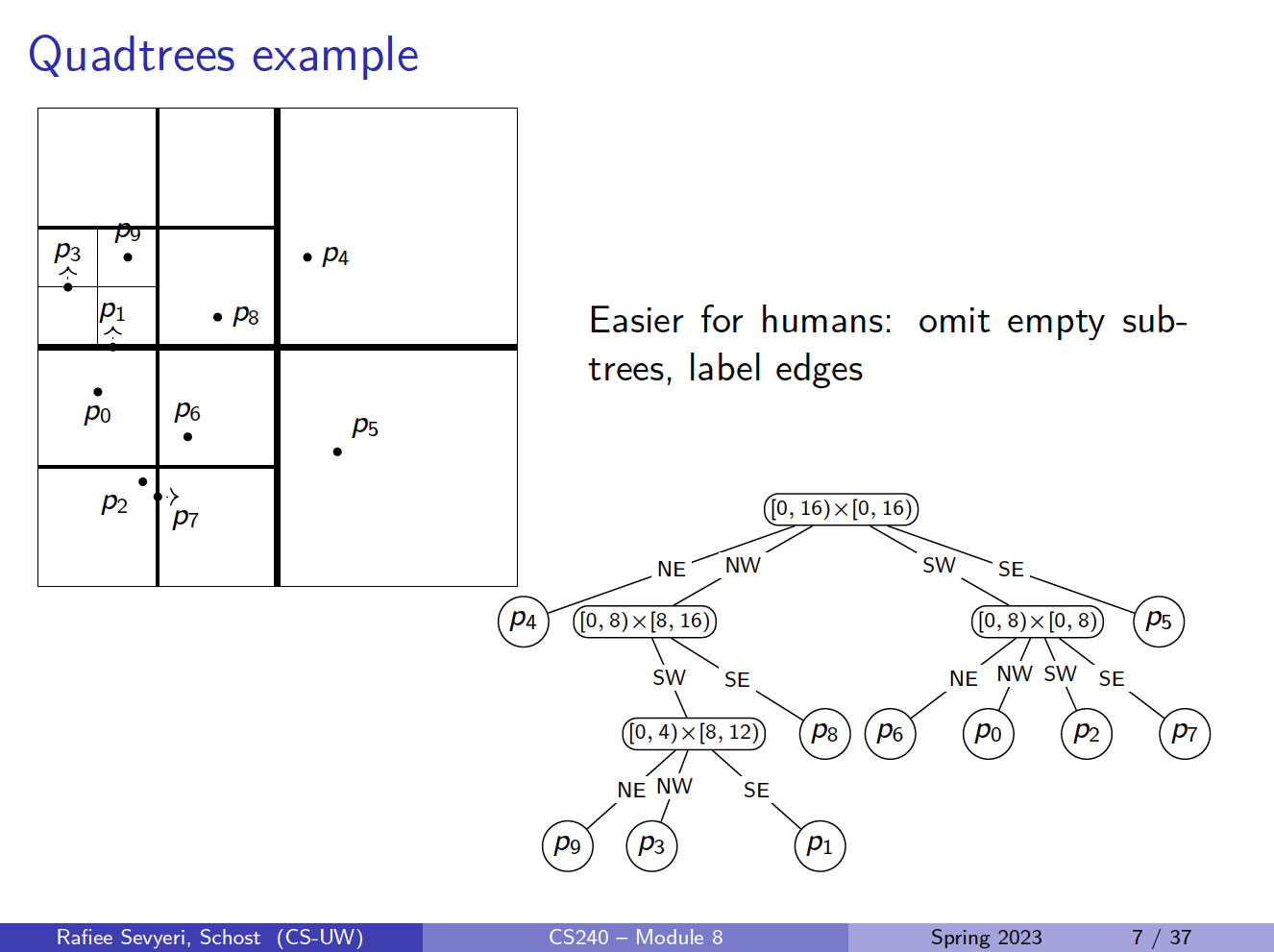
Structure (and also how to build the quadtree that stores $S$ ):

Root $r$ of the quadtree is associated with region $R$
If $R$ contains 0 or 1 points, then root $r$ is a leaf that stores point
Else split: Partition $R$ into four equal subsquares (quadrants) $R_{NE}$ , $R_{N W}$ , $R_{S W}$ , $R_{SE}$
Partition $S$ into sets $S_{NE}$ , $S_{N W}$ , $S_{S W}$ , $S_{SE}$ of points in these regions
Recursively build tree $T_{i}$ for points $S_{i}$ in region $R_{i}$ and make them children of the root