Range Search

Range Tree

First introduced in CS240.

Both Quadtrees and kd-Trees are intuitive and simple. However, they both may be very slow for range searches. Quadtrees are also potentially wasteful in space.

This is where we introduce Range trees, a “Tree of trees”.

Primary structure: Balanced binary search tree $T$ that stores $P$ and uses $x$-coordinates as keys.

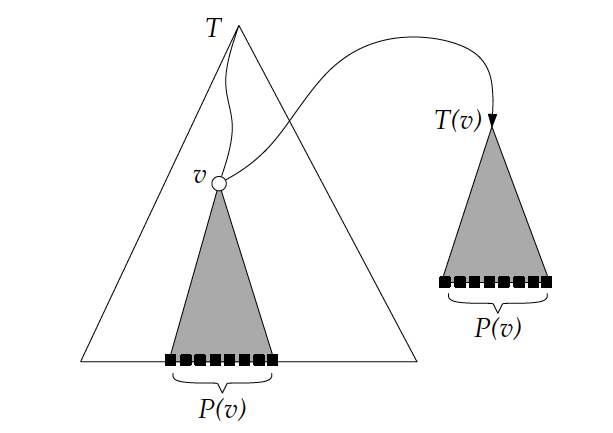
Every node $v$ of $T$ stores an associate structure $T(v)$:

• Let $P(v)$ be all points in subtree of $v$ in $T$ (including point at $v$)
• $T(v)$ stores $P(v)$ in a balanced binary search tree, using the $y$-coordinates as key
• Note: $v$ is not necessarily the root of $T(v)$

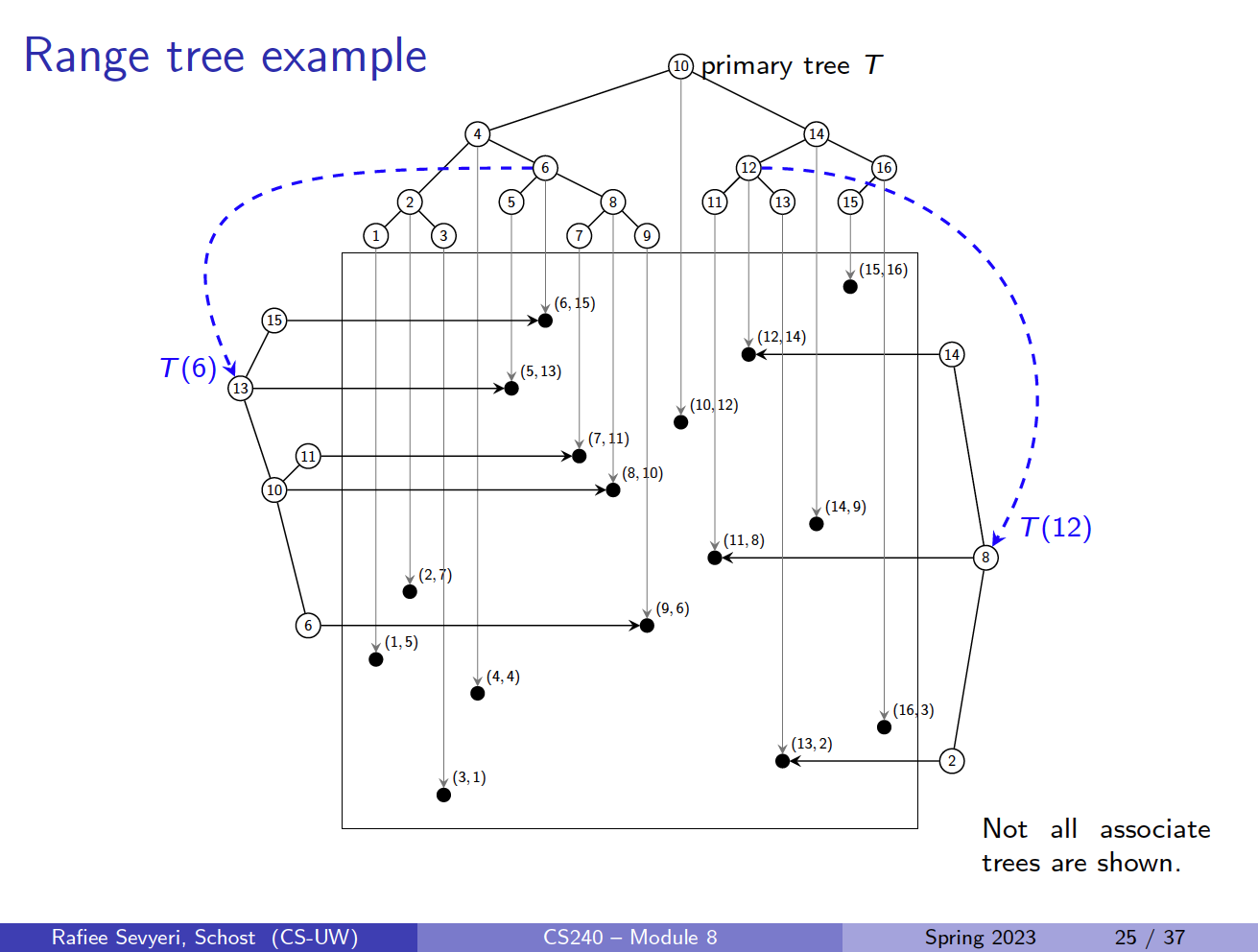
• These operations are a little hard to wrap your ahead around, but make sure to understand

First, you must understand how range search works on BSTs.

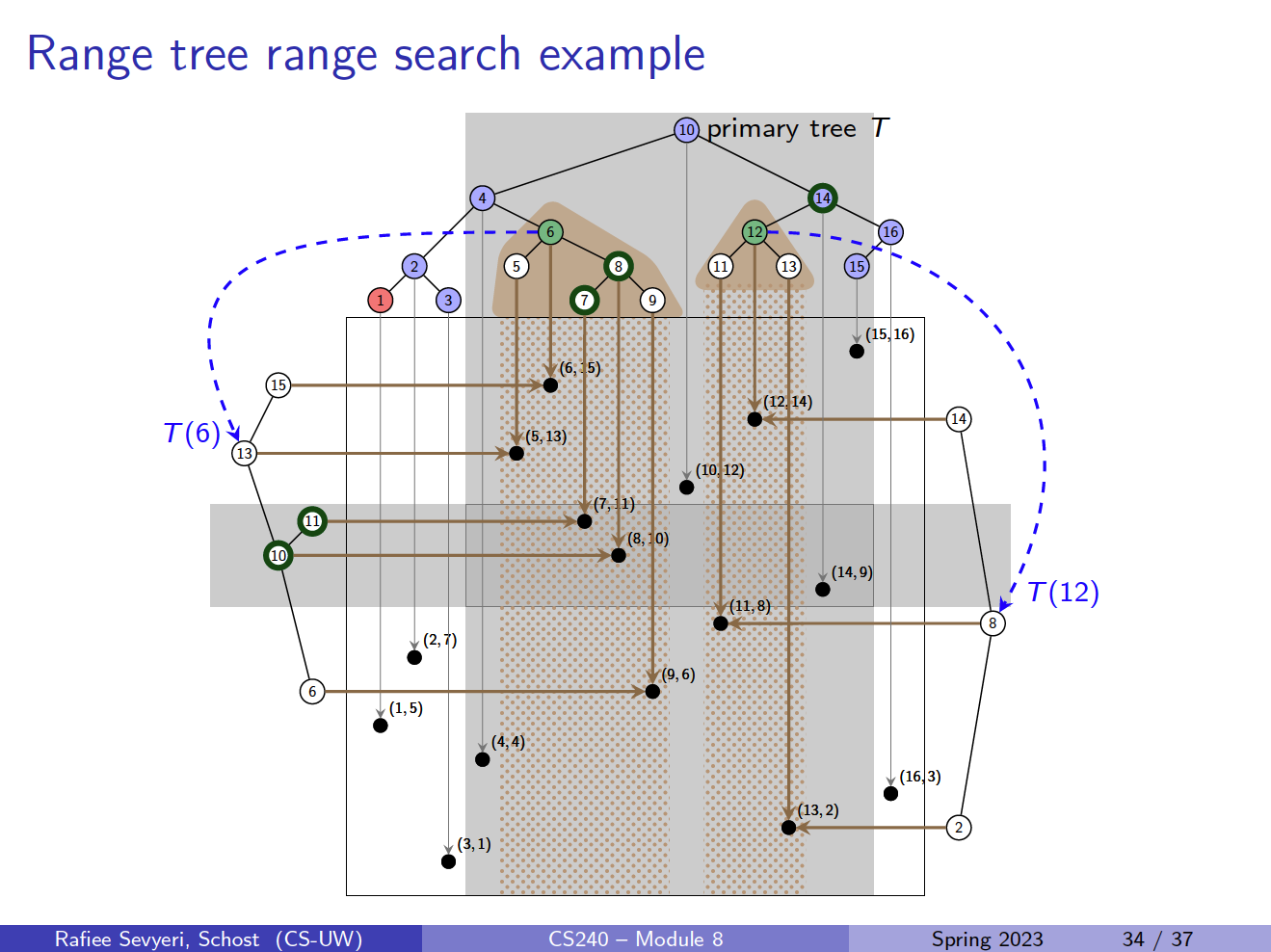
But the coolest part about range trees is being able to do range search, which you can do like this:

• AHHH YES, I GET IT LETS GOOOO I UNDERSTAND HOW THIS WORKSSS

When to use Quadtrees vs. kd-Trees vs Range Trees?

They are all Tradeoffs. Look at this set of slides: