Image Interpolation

Resampling

Notes from Cyrill Stachniss.

Resampling

Resampling refers to the process of changing the dimensions or geometry of an image.

Resampling is performing a discretization and quantization.

When is resampling actually used?

• Image zooming
• Rotation of image
• Geometry tranformations (skewing, warping, perspective transformions)

What is the problem that resampling is solving?

These transformations that we are applying on images lead to non-integer coordinates.

To assign intensity values from the input to the output images, we need to interpolate.

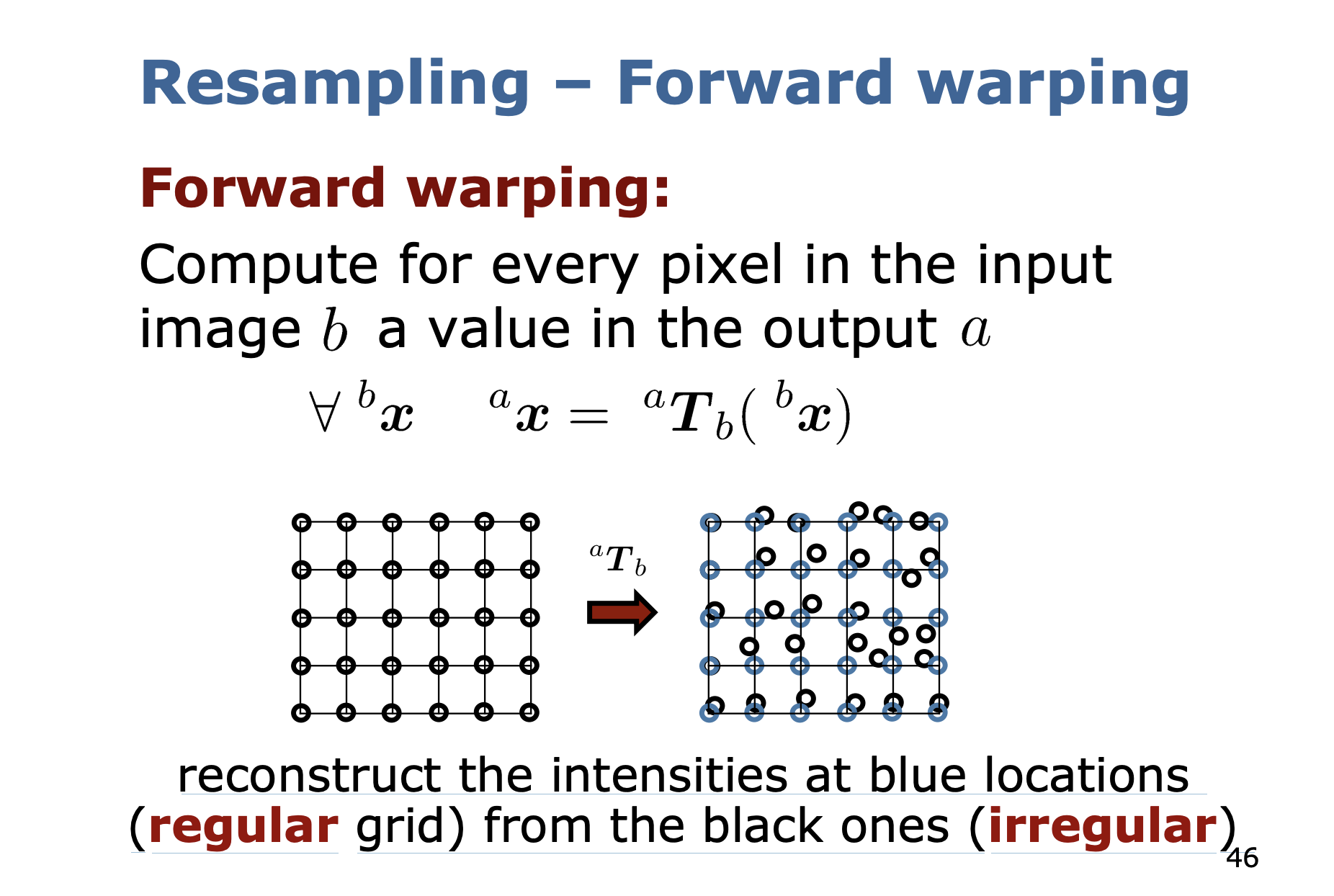
Resampling - Forward Warping

• Compute for every pixel in the input image $b$ a value in the output $a$

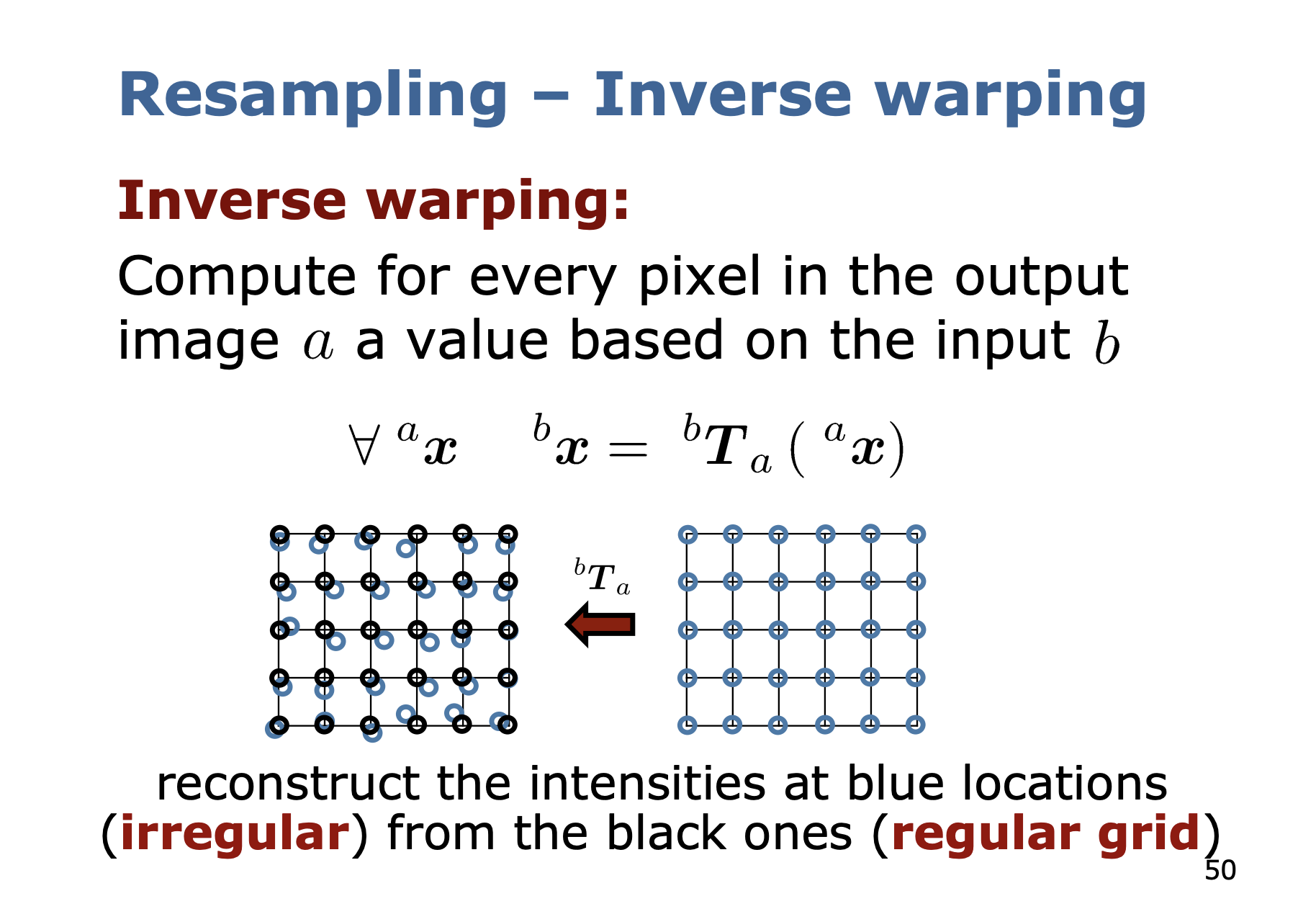
Inverse Warping

Forward or inverse warping?

Always use inverse warping!

• The forward approach can lead to missing pixels in the output image
• Inverse method allows for the direct application of bilin./cubic interpolation

You can get more complex warping behavior

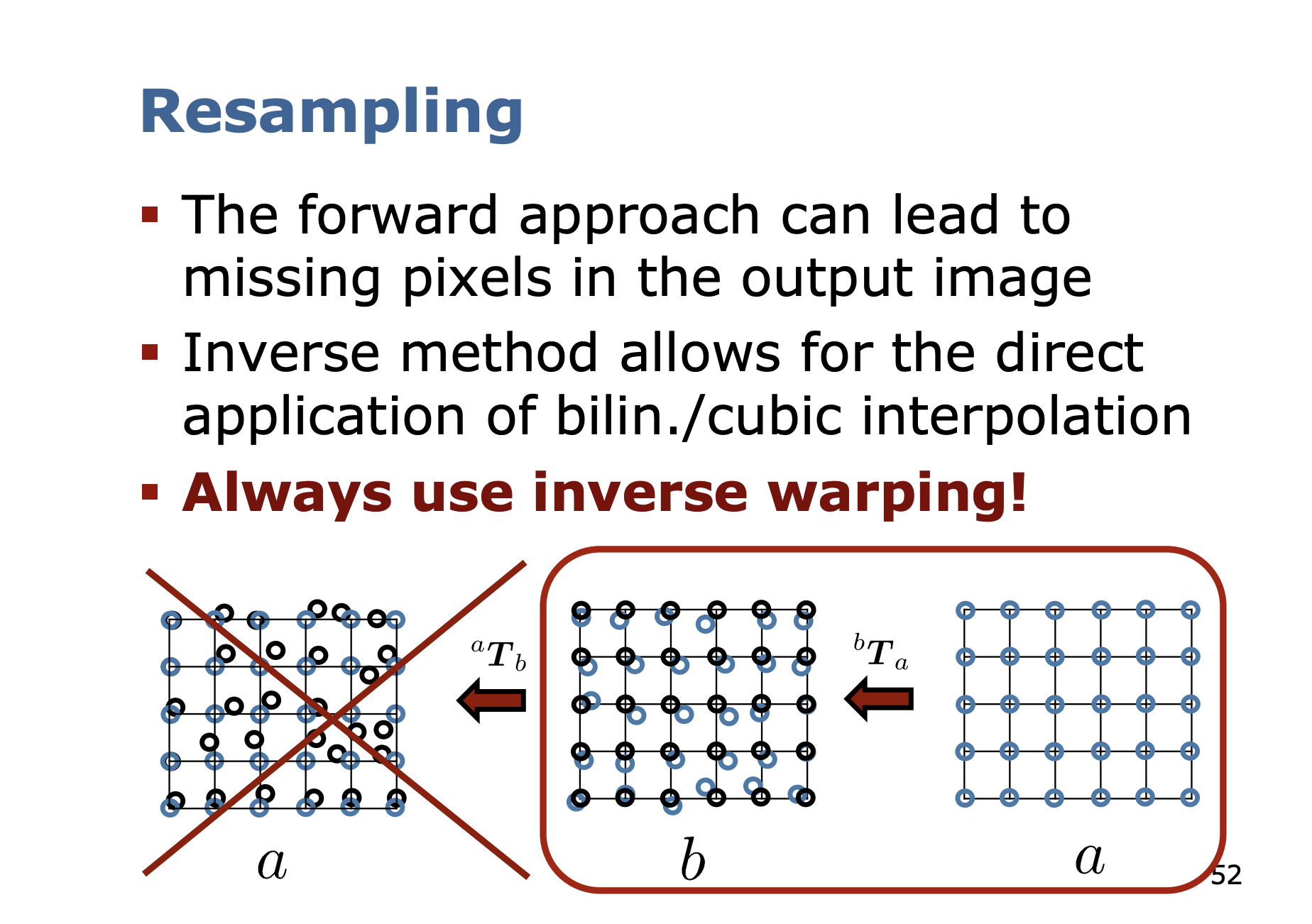
Image Half-Sizing

If you are taking half the size, you are neglecting information.

Use the $\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right]$ matrix to remap the pixel positions.

Through simple subsampling, we get aliasing artifacts.

Solution: Apply a Binomial Filter before subsampling.

Why is smoothing step needed?

• Simple subsampling results in aliasing and loosing details
• Smoothing combines pixel information from neighbouring pixels

This is the kernel that was used $B_2^{(2)}=\frac{1}{16}\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]$

How much smoothing is needed?

• Depends on the kernel
• Depends on the width of the kernel
• Depends on the scale of the transformation

Width of a kernel is given by its standard deviation.

$\sigma ={\left({\sum }_i{i}^{2}w(i)\right)}^{\frac{1}{2}}$

For the box filter ${}^{\sigma }{R}_n={\left(\frac{n^2-1}{12}\right)}^{\frac{1}{2}}$

For the binomial filter

${}^{\sigma }{B}_n={\left(\frac{n}{4}\right)}^{\frac{1}{2}}$

Scale of a Transformation

$m=\sqrt{\frac{1}{2}||\frac{\partial T}{\partial x}|{|}^2}$

where you have the following expansion

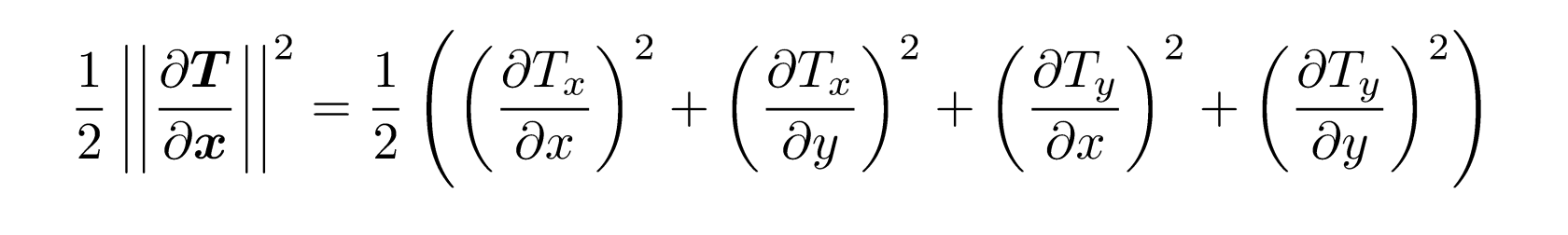
For the Gaussian filter

Consider the Scale for Resampling

• $m<1$: Image becomes smaller
  • Recommendation: $\sigma \approx m/2$
• $m=1$: Same scale
  • Use bilinear interpolation or bicubic for high quality results
• $m>1$: Image becomes larger
  • Use bicubic interpolation

What is the point of same scale case?

think about the rotation, or some shift that you want to take into account.