SE212

Semantic Tableaux

Semantic tableaux is another way of showing an argument is valid. We actually use negations to have everything come to a contradiction.

br = branching nb = non-branching

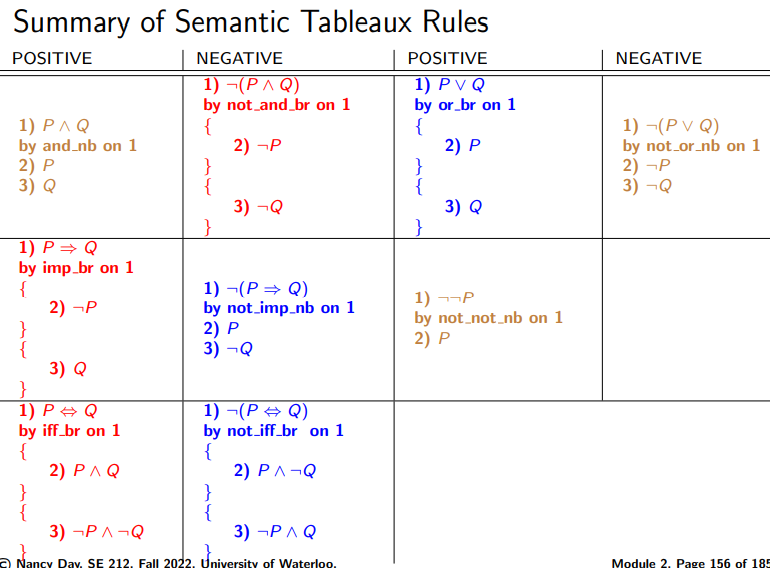
How to prove with Semantic Tableaux

• To show an argument is valid, we use a semantic tableau to show that $P_1,P_2,\dots ,P_N,\neg Q$ is an inconsistent set of formulas, i.e.
  • 1. premise
  • 2. premise
  • 3. negation of conclusion
• To prove that a set is Inconsistent Formula, just list out the premises and close everything
  • 1. premise
  • 2. premise

title: Heuristic for Semantic Tableaux
These are general tips for shorter proofs.
Propositional Logic: 
- Apply the non-branching rules first. 
 
Predicate Logic: 
- Apply the non-branching rules first. 
- When developing a semantic tableau in predicate logic, use the: existential quantification, and negative universal rules before the universal, and negative existential rule.
 
 

Examples

$\text{Prove that }\{b\wedge c,d,\neg (c\wedge d)\}\text{ is inconsistent}$

#check ST
b & c,  d, !(c & d) |- false
 
1) b & c
2) d
3) !(c & d)
by and_nb on 1
4) b
5) c
by not_and_br on 3
{
	6)  !c
	closed on 5,6
}
{
	7) !d
	closed on 2,7
}

To prove that an argument is valid

#check ST
p & q | r |- !p => r
 
1) p & q | r
2) !(!p => r)
...

1) a450 | bsup | !(a450 & bsup) by lem
2) case a450 | bsup {
3) conclusion by or_i on 2
}
4) Case !(a450 & bsup) {
5) a290 | !a290 by lem
6) case a290 {
7) conclusion by or_i on 6
}
8) case !a290 {
9) !a290 | !(a450 & bsup)} }
10) conclusion by or_i on 9
}
11) conclusion by cases on 5,6-7, 9-10
12) conclusion by cases on 1, 2-3, 4-11

$a290|!a290|!(a450\wedge bsup)\vee a450\wedge bsup<->true$ <→ a290 | !(a290 | a450 & bsup) | a450 & bsup by dm <→ a290 | a450 | bsup | !(a290 | a450 & bsup) <→ true by lem

$|=\neg (a290\wedge a450\wedge bsup)$ Recognize that the above formula is not a Tautology.

!(a290 & a450)
1) !(a290 & a450)
2) !!(a290 & a4580 & bsup)
by not_not_nb on 2
3) a290 & a450 & bsup
by and_nb on 3
4) a290 & a450
5) bsup
closed on 1,4
6)