Visibility Graph

I think I first got introduced to this with the UPenn Robotics course.

A visibility graph is a graph where each vertex represents an object or a point, and edges between vertices represent unobstructed lines of sight between them.

We can compute the shortest path between two points in a 2D space with obstacles by using the visibility graph of the obstacles.

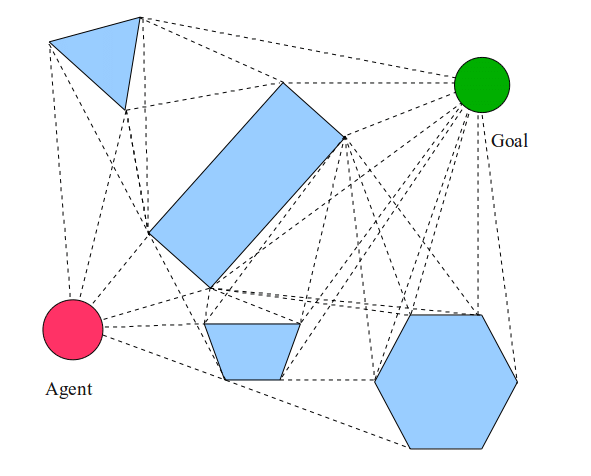
Note: In practice, we may want to pretend that the robot is actually a bit bigger than it truly is. This would inflate the configuration space obstacles by a safety margin so our trajectory doesn’t clip the obstacles so closely.

Once we’ve constructed the Visibility Graph, we can readily solved for the shortest path using Grassfire, Dijkstra, or the A* algorithm.

This visibility graph algorithm is complete (i.e. it will find a path if one exists and report failure if no path can be constructed).