Asymptotic Analysis

Learned in CS240, did a formal study of Big O.

Smaller / Larger Asymptotic Bounds

$\mathcal{O}$-notation: $f(n)\in O(g(n))$ ($f$ is asymptotically bounded above by $g)$ if there exist constants $c>0$ and $n_0\ge 0$ such that $|f(n)|\le c|g(n)|$ for all $n\ge n_0$.

$\Omega$-notation: $f(n)\in \Omega (g(n))$ (f is asymptotically bounded below by $g)$ if there exist constants $c>0$ and $n_0\ge 0$ such that $c|g(n)|\le |f(n)|$ for all $n\ge n_0$.

$\Theta$-notation: $f(n)\in \Theta (g(n))$ ($f$ is asymptotically tightly bounded by $g$) if there exist constants $c_1,c_2>0$ and $n_0\ge 0$ such that $c_1|g(n)|\le |f(n)|\le c_2|g(n)|$ for all $n\ge n_0$.

• This is usually what we talk about in Leetcode interviews $f(n)\in \Theta (g(n))⟺f(n)\in O(g(n))\text{ and }f(n)\in \Omega (g(n))$

Do NOT get confused

For some reason, I used to think that $\Omega$ was synonymous with “best case”, $O$ was the same as “worst case” , and $\Theta$ was the “average case”. This is misleading. For each case, you can calculate $\Omega ,O,\Theta$.

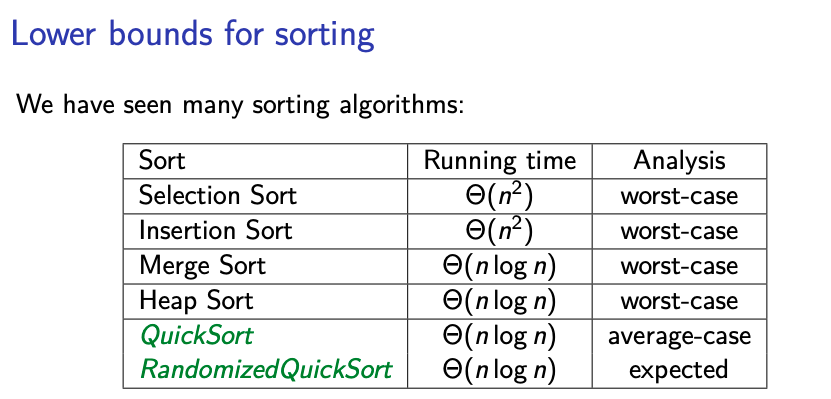
Maybe the confusion comes from the Sorting Algorithms page (yea…)

Strictly Smaller / Larger Asymptotic Bounds

$\omega$-notation: $f(n)\in \omega (g(n))$ (f is asymptotically strictly larger than $g$) if for all constants $c>0$, there exists a constant $n_0\ge 0$ such that $|f(n)|\ge c|g(n)|$ for all $n\ge n_0$.

$o$-notation: $f(n)\in o(g(n))$ (f is asymptotically strictly smaller than $g$) if for all constants $c>0$, there exists a constant $n_0\ge 0$ such that $|f(n)|\le c|g(n)|$ for all $n\ge n_0$.

Notes

• Main difference to $O$, $\Omega$ is the quantifier for $c$.
• Rarely proved from first principles.

Algebra of Order Notations

Identity rule: $f(n)\in \Theta (f(n))$

Transitivity:

• If $f(n)\in O(g(n))$ and $g(n)\in O(h(n))$ then $f(n)\in O(h(n))$
• If $f(n)\in \Omega (g(n))$ and $g(n)\in \Omega (h(n))$ then $f(n)\in \Omega (h(n))$

Maximum rules: Suppose that $f(n)>0$ and $g(n)>0$ for all $n\ge n_0$. Then:

• $f(n)+g(n)\in O(\max \{f(n),g(n)\})$
• $f(n)+g(n)\in \Omega (\max \{f(n),g(n)\})$

Techniques for Order Notation