Big-O Notation

Big O is useful to write code considering optimization. Also see Asymptotic Analysis for content covered from CS240.

Competitive Programming

$n$	Big-$\mathcal{O}$ Upper Bound
$n\le 10$	$\mathcal{O}(n!)$
$n\le 20$	$\mathcal{O}(2^n)$
$n\le 50$	$\mathcal{O}(n^5)$
$n\le 100$	$\mathcal{O}(n^4)$
$n\le 500$	$\mathcal{O}(n^3)$
$n\le 3000$	$\mathcal{O}(n^2\cdot \log n)$
$n\le 5000$	$\mathcal{O}(n^2)$
$n\le 10^5$	$\mathcal{O}(n\cdot \log n)\sim \mathcal{O}(n\cdot \sqrt{n})$
$n\le 10^6$	$\mathcal{O}(n\cdot \log n)\sim \mathcal{O}(n)$
$n\le 10^{12}$	$\mathcal{O}(\sqrt{n})$
$n\le 10^{18}$	$\mathcal{O}(\log n)$

Math

Definition from MATH119

Given two functions $f$ and $g$, we say that “$f$ is of order $g$ as $x\to x_0$” and write $f(x)=O(g(x))\text{as }x\to x_0$ if there exists a constant $A$ (greater than zero) such that $|f(x)|\le A|g(x)|$ on some interval around $x_0$ (although the point $x_0$ itself may be excluded from the interval, since the idea is to describe the behaviour of $f$ in the limit as we approach $x_0$).

In computer science, we deal with behaviour as $n\to \infty$ instead of $x\to x_0$.

• Ahh, but actually, there are 3 different types of bounds ($O$, $\Omega$ and $\Theta$). Upper, lower, and and tight bounds. Ahh see Asymptotic Analysis, which I learned in CS240.

Time Complexity

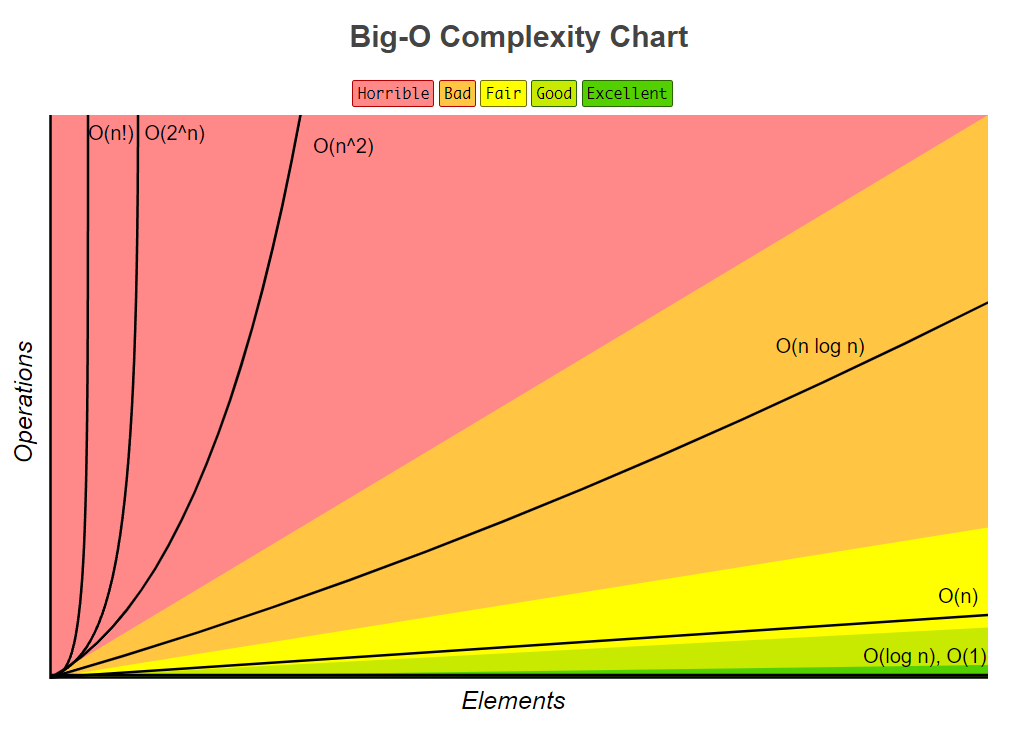
Common Growth Rates (from CS240):

• $O(1)$ $\to$ Constant-time algorithm
• $O(\log n)$ $\to$ Logarithmic algorithm
• $O(\sqrt{n})$ $\to$ Square Root algorithm
• $O(n)$ $\to$ Linear Algorithm
• $O(n\log n)$ $\to$ Linearithmic Algorithm
• $O(n{\log }^{k}n)$ for some constant $k$ $\to$ quasi-linear Algorithm
• $O(n^2)$ $\to$ Quadratic Algorithm, usually two nested loops
• $O(n^3)$ $\to$ Cubic Algorithm, usually three nested loops
• $O(2^n)$ $\to$ Exponential Algorithm, iterates through all subsets of input elements
• $O(n!)$ $\to$ Algorithm iterates through all permutations of the input elements

See Amortized Analysis

Space Complexity

Similar idea to time complexity but relating to how much memory a particular problem takes to run.

Algebra of Big O

1. $kO(x^n)=O(x^n),\text{for any constant }k$
2. $O(x^m)+O(x^n)=O(x^q),\text{where }q=\min (m,n)$
3. $O(x^m)\cdot O(x^n)=O(x^{m+n})$
4. $[O(x^n){]}^m=O(x^{mn})$
5. $\frac{O(x^m)}{x^n}=O(x^{m-n})$

Note that we cannot state a general rule for simplifying $\frac{O(x^m)}{O(x^n)}$

Personal Experimentation

I did a cycle cost analysis (like how much each cycle costs) while working at Ericsson, and I wanted to understand how much slower each function is.

Related

• Asymptotic Analysis
• Amortized Analysis