Cache Blocking / Tiling

Tiling makes use of CUDA Shared Memory so that you reduce the amount of times you are reading from global memory when executing a CUDA kernel.

Introduced to me through this article https://siboehm.com/articles/22/Fast-MMM-on-CPU

This is the MOST FUNDAMENTAL thing, introduced in chapter 4.4 of PMPP.

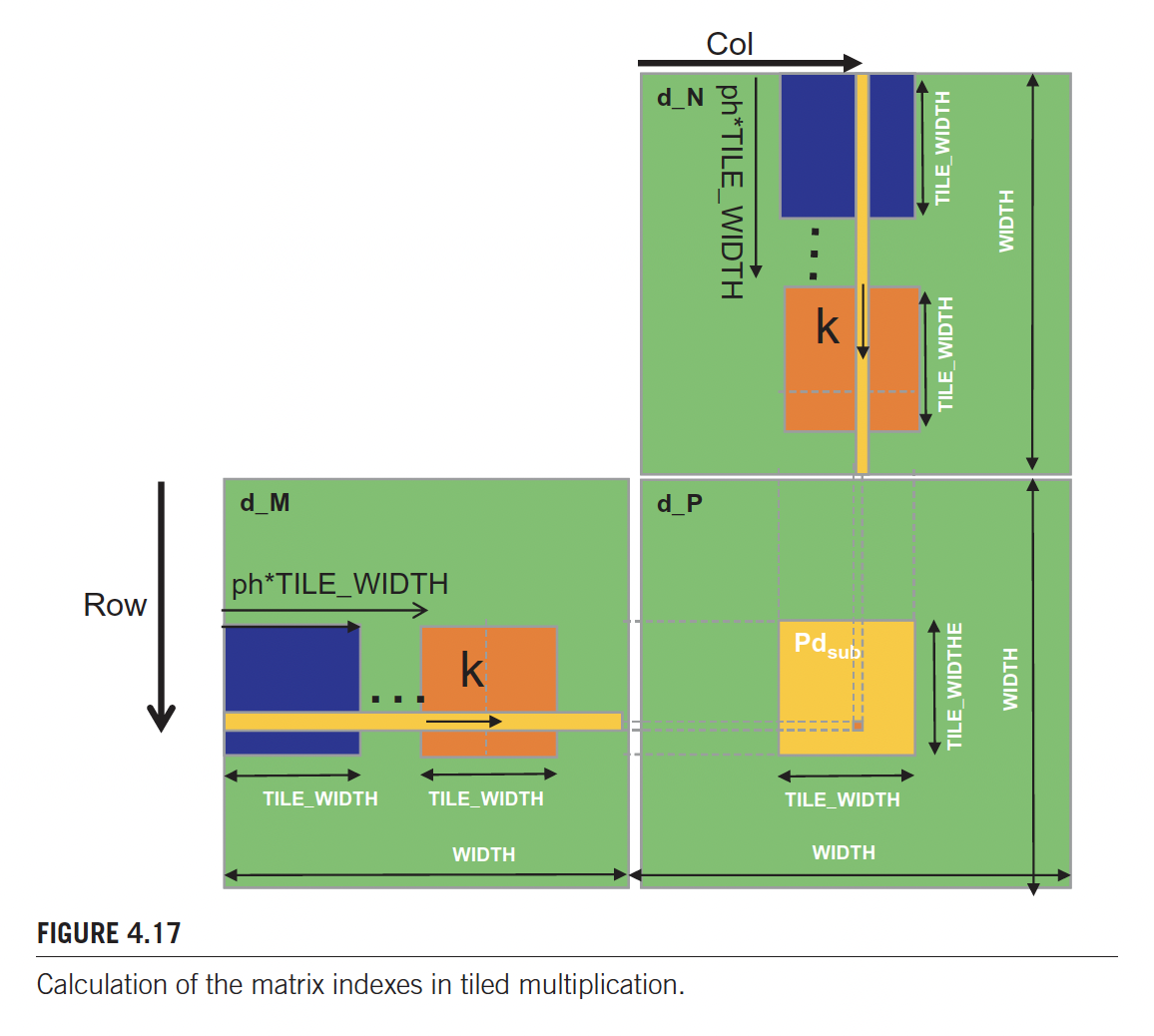
With tiled matrix multiplication, threads to collaboratively load subsets of the $M$ and $N$ elements into the shared memory before they individually use these elements in their dot product calculation.

__global__ void MatrixMulKernel(float* d_M, float* d_N, float* d_P,
int Width) {
  __shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
  __shared__ float Nds[TILE_WIDTH][TILE_WIDTH];
  int bx = blockIdx.x; int by = blockIdx.y;
  int tx = threadIdx.x; int ty = threadIdx.y;
  // Identify the row and column of the d_P element to work on
  int Row = by * TILE_WIDTH + ty;
  int Col = bx * TILE_WIDTH + tx;
  float Pvalue = 0;
  // Loop over the d_M and d_N tiles required to compute d_P element
  for (int ph = 0; ph < Width/TILE_WIDTH; ++ph) {
  // Collaborative loading of d_M and d_N tiles into shared memory
  Mds[ty][tx] = d_M[Row*Width + ph*TILE_WIDTH + tx];
  Nds[ty][tx] = d_N[(ph*TILE_WIDTH + ty)*Width + Col];
  __syncthreads();
  for (int k = 0; k < TILE_WIDTH; ++k) {
  Pvalue += Mds[ty][k] * Nds[k][tx];
  }
  __syncthreads();
  }
  d_P[Row*Width + Col] = Pvalue;
}

I don’t get the names though

• d_M = matrix M on device memory (GPU)
  • so I assume h_M means matrix M on host memory (CPU)
• Mds = Md shared, M on device

Reading this code

You can see that the shared memory is done across a block.

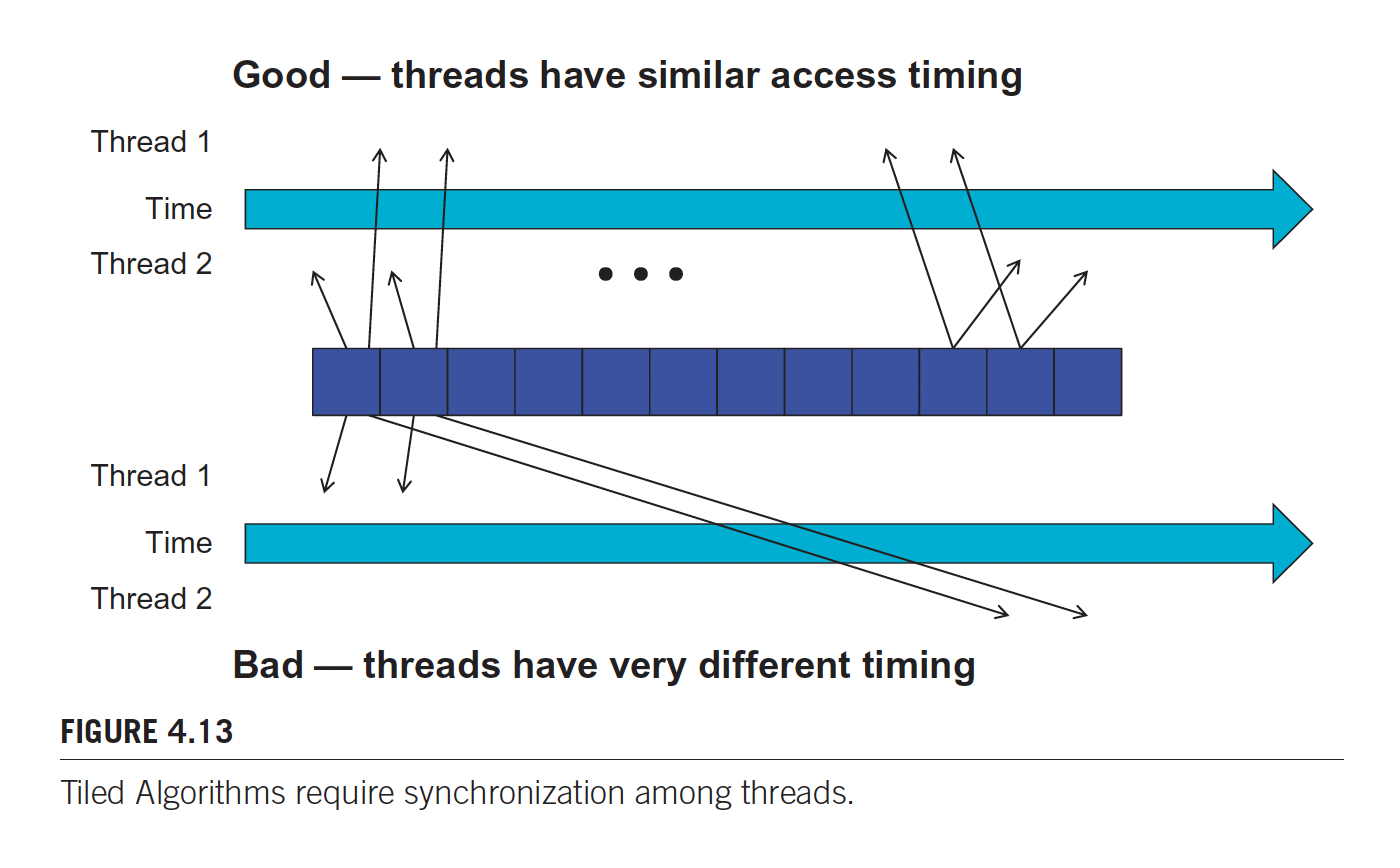
Notice that there are 2 __syncthreads() calls. Each of them serve a different purpose.

Line 11 ensures that all threads have finished loading the tiles of M and N into Mds and Nds before any of them can move forward.

Second call: Ensures that threads have finished using the M and N elements in the shared memory before any of them move on to the next iteration and load the elements from the next tiles. In this manner, none of the threads would load the elements too early and corrupt the input values for other threads.

The kernel cannot easily adjust its shared memory usage at runtime without recompilation.

Boundary Checks

We add boundary checks for tiling in the event of uneven matrices.

// Loop over the M and N tiles required to compute P element
for (int ph = 0; ph < ceil(Width/(float)TILE_WIDTH); ++ph) {
// Collaborative loading of M and N tiles into shared memory
if ((Row< Width) && (ph*TILE_WIDTH+tx)< Width)
  Mds[ty][tx] = M[Row*Width + ph*TILE_WIDTH + tx];
  if ((ph*TILE_WIDTH+ty)<Width && Col<Width)
  Nds[ty][tx] = N[(ph*TILE_WIDTH + ty)*Width + Col];
   __syncthreads();
  for (int k = 0; k < TILE_WIDTH; ++k) {
  Pvalue += Mds[ty][k] * Nds[k][tx];
  }
   __syncthreads();
}
 if ((Row<Width) && (Col<Width)P[Row*Width + Col] = Pvalue;