Camera

Camera Lens Distortion

Distortion (notes from Visual SLAM book)

There are some mathematical models to describe the distortion caused by the shape of the lens.

There are 2 types of distortion that I was introduced to (the Rad-tan model):

1. radial distortion is introduced by the shape of the lens
2. tangential distortion is introduced during assembly of the camera because the lens and the imaging surface cannot be strictly parallel

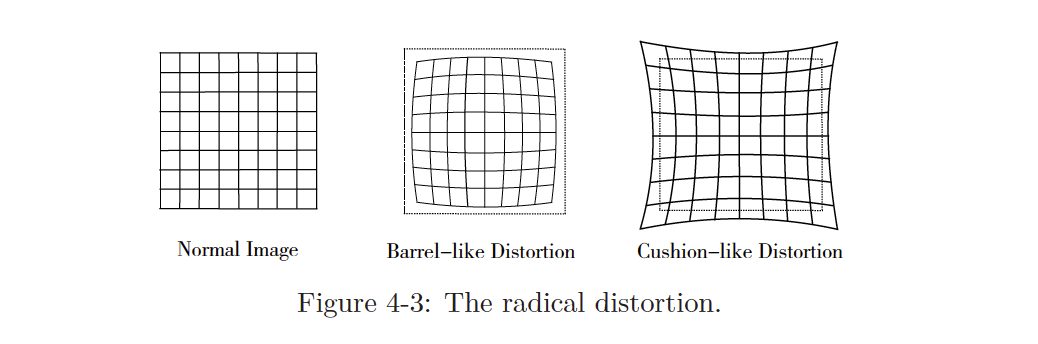
Radial Distortion

In order to get a larger FoV (Field-of-View), we usually add a lens in front of the camera.

• oohhh is that the point of lenses? I didn’t think about ti that way before

A byproduct of this is that in photos, the straight lines become more curved the closer these are to the edge of the image. You know this learning the types of Camera Shots.

Radial distortion is radially symmetrical.

2 categories of distortion:

• barrel-like distortion
• cushion-like distortion (where do you ever get this??)

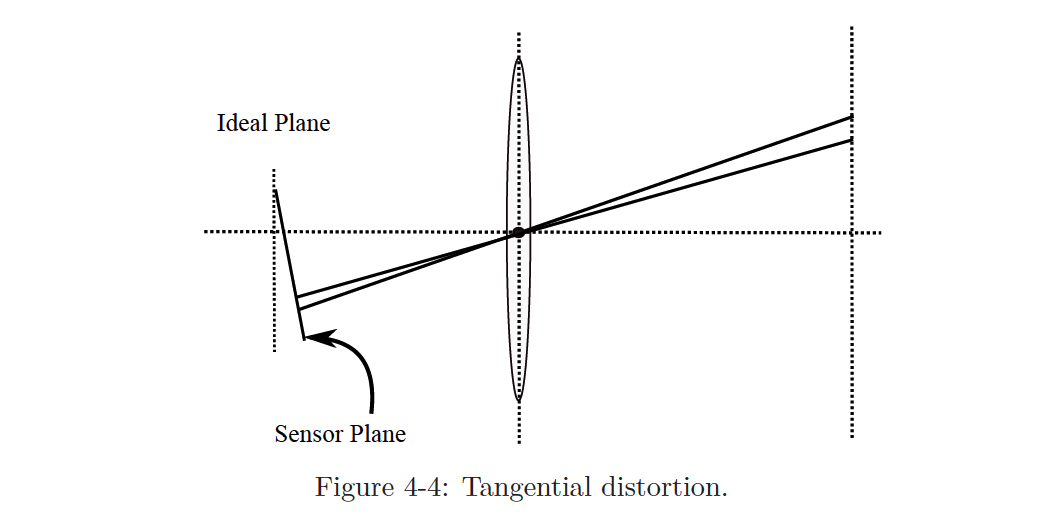
Tangential Distortion

Tangential distortion is introduced during assembly of the camera because the lens and the imaging surface cannot be strictly parallel.

Formal Math

Consider any point on the normalized plane, $\mathbf{p}$, whose coordinates are $[x,y{]}^T$, or $[r,\theta {]}^T$ in the form of polar coordinates, where $r$ represents the distance between the point $\mathbf{p}$ and the origin of the coordinate system, and $\theta$ represents the angle to the horizontal axis.

Radial distortion can be seen as a change in the coordinate point along the length, that is, its radius from the origin.

Tangential distortion can be seen as a change in the coordinate point along the tangential direction, which means that the horizontal angle has changed. It is generally assumed that these distortions are polynomial, namely:

\begin{matrix} x_\mathrm{distorted} = x(1+k_1r^2+k_2r^4+k_3r^6)\\ y_\mathrm{distorted} = y(1+k_1r^2+k_2r^4+k_3r^6) \end{matrix}, \end{equation}

• $[x_{\mathrm{distorted}},y_{\mathrm{distorted}}{]}^T$ is the normalized coordinates of the point after distortion.

For tangential distortion, we can use the other two parameters $p_1,p_2$ to describe it:

\begin{equation} \begin{matrix} x_\mathrm{distorted} = x+2p_1xy+p_2(r^2+2x^2)\\ y_\mathrm{distorted} = y+p_1(r^2+2y^2)+2p_2xy \end{matrix}. \end{equation}$$ Putting the two types of distortions together we get a joint model with 5 distortion coefficients. The complete form is: $$\begin{equation} \left\{\begin{matrix} x_\mathrm{distorted} =x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)\\ y_\mathrm{distorted} = y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy \end{matrix}\right. . \end{equation}

From Cyrill Stachniss lectures

Aberrations

A deviation from the ideal mapping with a thin lens is called aberration. Main types of aberrations:

• Distortion
• Spherical aberrations
• Chromatic aberrations
• Astigmatism
• Comatic aberrations
• Vignetting
• …

• Also see Plumb Bob Model

• Ohh my actual eyes have the same problem