Camera

Pinhole Camera Geometry

oh my god, all my lessons with Optics in high school is coming back…

• Learned from the Visual SLAM book, starting page 96
• I also have notes that I understand better in Camera Calibration, which I learned from Cyrill stachniss.

Camera Calibration

• Camera Intrinsics
• Camera Extrinsics

Camera Distortion

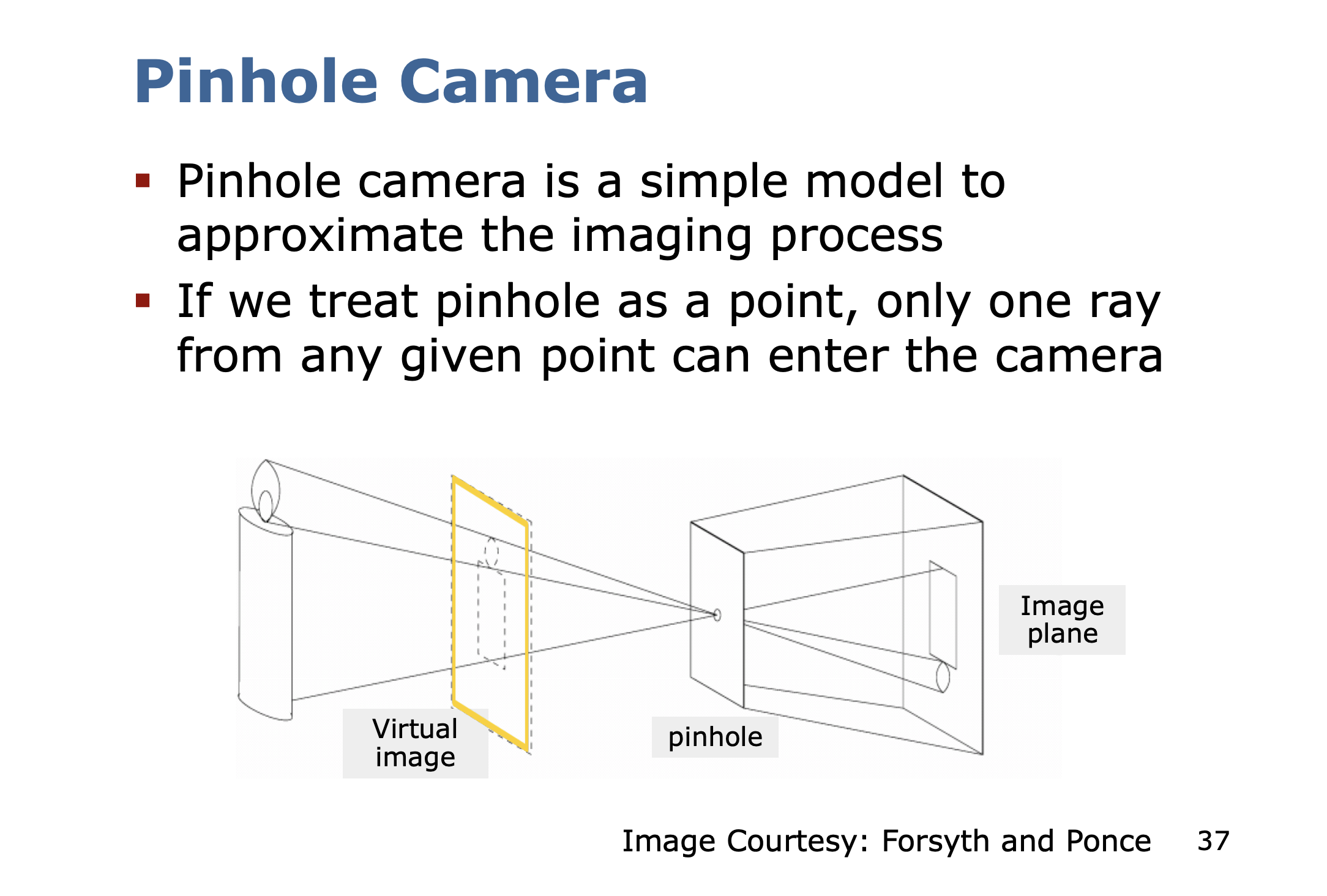
Summary

Let’s summarize the imaging process of a monocular camera:

1. First, there is a point $P$ in the world coordinate system, and its world coordinates are ${\mathbf{P}}_w$.
2. Since the camera is moving, its motion is described by $\mathbf{R},\mathbf{t}$ or transform matrix $\mathbf{T}\in \mathrm{SE}(3)$. The camera coordinates for $P$ are ${\tilde{\mathbf{P}}}_c=\mathbf{R}{\mathbf{P}}_w+\mathbf{t}$.
3. The ${\tilde{\mathbf{P}}}_c$ components are $X,Y,Z$, and they are projected onto the normalized plane $Z=1$ to get the normalized coordinates: ${\mathbf{P}}_c=[X/Z,Y/Z,1{]}^T$. Note that $Z$ may be less than 1, indicating that the point is behind the normalization plane and it should not be projected on the camera plane.
4. If the image is distorted, the coordinates of ${\mathbf{P}}_c$ after distortion are calculated according to the distortion parameters.
5. Finally, the distorted coordinates of $P$ pass through the intrinsics and we find its pixel coordinates: ${\mathbf{P}}_{uv}=\mathbf{K}{\mathbf{P}}_c$.