Linear Diophantine Equation

Congruence and Modular Arithmetic

Invented/Discovered by Carl Friedrich Gauss.

Let $m$ be a fixed positive integer. For integers $a$ and $b$, we say that $a$ is congruent to $b$ modulo $m$, and write

$a\equiv b(\mathrm{mod}m)$ when $m\mid (a-b)$. For integers $a$ and $b$ such that $m\nmid (a-b)$, we write $a\not\equiv b(\mathrm{mod}m)$. We refer to $\equiv$ as congruence, and $m$ as its modulus.

Competitive Programming

See Modular Inverse.

MATH135

Elementary Properties of Congruence

One convenient aspect of congruence is that it behaves a lot like equality. For example, equality is an equivalence relation on the integers. This means that it has the following three properties:

1. Reflexivity: For all integers $a$, $a=a$.
2. Symmetry: For all integers $a$ and $b$, $a=b⟺b=a$.
3. Transitivity: For all integers $a$,$b$ and $c$, $(a=b)\wedge (b=c)⟹(a=c)$.

Equivalence relation Let $S$ be any set and let $\Delta$ be any binary relation on $S$. Then $\Delta$ is said to be an equivalence relation if “same thing as above”

Some Theorems

Congruence is an Equivalence Relation (CER) For all integers $a$, $b$ and $c$, we have

1. $a\equiv a(\mathrm{mod}m)$.
2. If $a\equiv b(\mathrm{mod}m)$, then $b\equiv a(\mathrm{mod}m)$.
3. If $a\equiv b(\mathrm{mod}m)$ and $b\equiv c(\mathrm{mod}m)$,then $a\equiv c(\mathrm{mod}m)$.

Proposition 2 For all integers $a_1$, $a_2$, $b_1$ and $b_2$, if $a_1\equiv b_1(\mathrm{mod}m)$ and $a_2\equiv b_2(\mathrm{mod}m)$, then

1. $a_1+a_2\equiv b_1+b_2(\mathrm{mod}m)$,
2. $a_1-a_2\equiv b_1-b_2(\mathrm{mod}m)$,
3. $a_1{a}_2\equiv b_1{b}_2(\mathrm{mod}m)$

Congruence Add and Multiply (CAM) For all positive integers $n$, for all integers $a_1,\dots ,a_n$, and $b_1,\dots ,b_n$, if $a_i\equiv b_i(\mathrm{mod}m)$ for all $1\le i\le n$, then

1. $a_1+a_2+\cdots +a_n\equiv b_1+b_2+\cdots +b_n(\mathrm{mod}m),$
2. $a_1{a}_2\cdots a_n\equiv b_1{b}_2\cdots b_n(\mathrm{mod}m)$.

Congruence Power (CP) For all positive integers $n$ and integers $a$ and $b$, if $a\equiv b(\mathrm{mod}m)$, then $a^n\equiv b^n(\mathrm{mod}m)$.

Congruence Divide (CD) For all integers $a$, $b$ and $c$, if $ac\equiv bc(\mathrm{mod}m)$and $\gcd (c,m)=1$, then $a\equiv b(\mathrm{mod}m)$.

Congruence and Remainders

Congruent Iff Same Remainder (CISR) For all integers $a$ and $b$, $a\equiv b(\mathrm{mod}m)$ if and only if $a$ and $b$ have the same remainder when divided by $m$.

Congruent To Remainder (CTR) For all integers $a$ and $b$ with $0\le b<m$, $a\equiv b(\mathrm{mod}m)$ if and only if $a$ has remainder $b$ when divided by $m$.

Linear Congruence

A relation of the form $ax\equiv c(\mathrm{mod}m)$ is called a linear congruence in the variable $x$. A solution to such a linear congruence is an integer $x_0$ such that $a{x}_0\equiv c(\mathrm{mod}m)$

title: #todo: How do i actually caldulate this?
see notes

Linear Congruence Theorem (LCT) For all integers $a$ and $c$, with a non-zero, the linear congruence $ax\equiv c(\mathrm{mod}m)$ has a solution if and only if $d\mid c$, where $d=\gcd (a,m)$. Moreover, if $x=x_0$ is one particular solution to this congruence, then the set of all solutions is given by

$\{x\in \mathbb{Z}:x\equiv x_0(\mathrm{mod}\frac{m}{d})\}$ or, equivalently, $\{x\in \mathbb{Z}:x\equiv x_0,x_0+\frac{m}{d},x_0+2\frac{m}{d},\dots ,x_0+(d-1)\frac{m}{d}(\mathrm{mod}m)\}$

Non-Linear Congruence#gap-in-knowledge

For higher powers, we can solve a congruence relation modulo $m$ by checking all $m$ values, which works quite well when $m$ is small. (so essentially brute forcing)

Congruence Classes and Modular Arithmetic

The congruence class modulo $m$ of the integer $a$ is the set of integers $[a]=\{x\in \mathbb{Z}:x\equiv a(\mathrm{mod}m)\}$

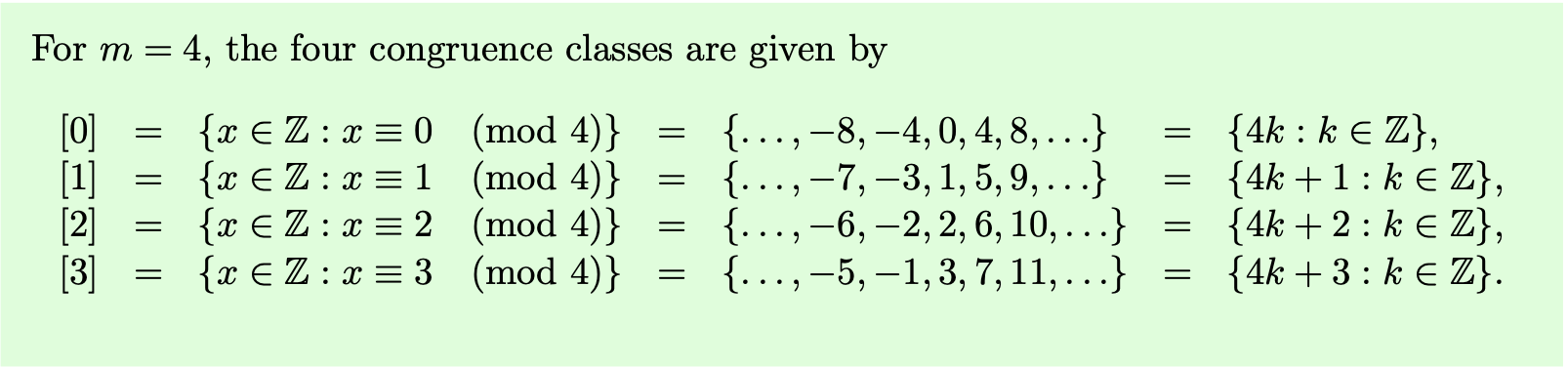
We define ${\mathbb{Z}}_m$ to be the set of ${\mathbb{Z}}_m$ congruence classes
${\mathbb{Z}}_m=[0],[1],[2],\dots ,[m-1]$ and we define two operations on ${\mathbb{Z}}_m$, addition and multiplication, as follows: $[a]+[b]=[a+b]$ $[a][b]=[ab]$

When we apply these operations on the set ${\mathbb{Z}}_m$, we are doing what is known as modular arithmetic.

Inverses in ${\mathbb{Z}}_m$ (INV ${\mathbb{Z}}_m$)

I really struggled with this for MATH135. See MATH135. See Modular Multiplicative Inverse Inverse defintiion

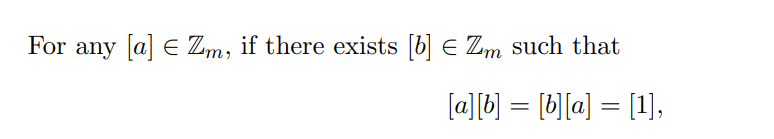
Let $a$ be an integer with $1\le a\le m-1$. The element $[a]$ in ${\mathbb{Z}}_m$ has a multiplicative inverse if and only if $\gcd (a,m)=1$. Moreover, when $\gcd (a,m)=1$, the multiplicative inverse is unique.

Inverses in ${\mathbb{Z}}_p$ (INV ${\mathbb{Z}}_p$)

For all prime numbers $p$ and non-zero elements [a] in ${\mathbb{Z}}_p$, the multiplicative inverse $[a{]}^{-1}$ exists and is unique.

Fermat’s Little Theorem (F$l$T)

For all prime numbers $p$ and integers $a$ not divisible by $p$, we have $a^{p-1}\equiv 1(\mathrm{mod}p)$

Corollary for Fermat’s Little Theorem

$a^p\equiv a(\mathrm{mod}p)$

Chinese Remainder Theorem (CRT)

For all integers $a_1$ and $a_2$, and positive integers $m_1$ and $m_2$, if $\gcd (m_1,m_2)=1$, then the simultaneous linear congruences $n\equiv a_1(\mathrm{mod}{m}_1)$ $n\equiv a_2(\mathrm{mod}{m}_2)$

have a unique solution modulo $m_1{m}_2$. Thus, if $n=n_0$ is one particular solution, then the solutions are given by the set of all integers $n$ such that

$n\equiv n_0(\mathrm{mod}{m}_1{m}_2)$

Generalized Chinese Remainder Theorem (GCRT)

For all positive integers $k$ and $m_1,m_2,\dots ,m_k$, and integers $a_1,a_2,\dots ,a_k$, if $\gcd (m_i,m_j)=1$ for all $i\ne j$, then the simultaneous congruences

$n\equiv a_1(\mathrm{mod}{m}_1)$ $n\equiv a_2(\mathrm{mod}{m}_2)$ $⋮$ $n\equiv a_k(\mathrm{mod}{m}_k)$ have a unique solution modulo $m_1,m_2,\dots ,m_k$. Thus, if $n=n_0$ is one particular solution, then the solutions are given by the set of all integers $n$ such that $n\equiv n_0(\mathrm{mod}{m}_1{m}_2\dots m_k)$

Splitting Modulus Theorem (SMT)

For all integers $a$ and positive integers $m_1$ and $m_2$, if $\gcd (m_1,m_2)=1$, then the simultaneous congruences $n\equiv a(\mathrm{mod}{m}_1)$ $n\equiv a(\mathrm{mod}{m}_2)$

have exactly the same solutions as the single congruence $n\equiv a(\mathrm{mod}{m}_1{m}_2)$.