Congruence and Modular Arithmetic

Modular Multiplicative Inverse

$a\cdot x\equiv 1\mathrm{mod}m$  Then, by definition, the modular inverse of  $a$  is  $x$ .

Consider the following equation (a LDE) with unknown $x,y$: $ax+my=1$

Competitive Programming

Needed to learn this after messing up this question https://codeforces.com/contest/2008/problem/F

Resources

• https://cp-algorithms.com/algebra/module-inverse.html

Modular Inverse % MOD

int inv(int a) {
  return a <= 1 ? a : MOD - (long long)(MOD/a) * inv(MOD % a) % MOD;
}

• https://cp-algorithms.com/algebra/module-inverse.html#mod-inv-all-num

This is used for Binomial Coefficient % MOD.

Using EEA without MOD

If you need the original one without modulo, use EEA.

This is calculated using EEA, where we have the function

int extended_euclidean(int a, int b, int& x, int& y) {
    x = 1, y = 0;
    int x1 = 0, y1 = 1, a1 = a, b1 = b;
    while (b1) {
        int q = a1 / b1;
        tie(x, x1) = make_tuple(x1, x - q * x1);
        tie(y, y1) = make_tuple(y1, y - q * y1);
        tie(a1, b1) = make_tuple(b1, a1 - q * b1);
    }
    return a1;
}

int x, y;
int g = extended_euclidean(a, m, x, y);
if (g != 1) {
    cout << "No solution!";
}
else {
    x = (x % m + m) % m;
    cout << x << endl;
}

MATH135

Inverses in ${\mathbb{Z}}_m$ (INV ${\mathbb{Z}}_m$)

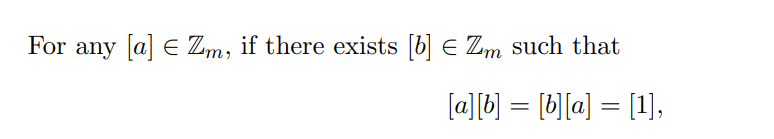
Let $a$ be an integer with $1\le a\le m-1$. The element $[a]$ in ${\mathbb{Z}}_m$ has a multiplicative inverse if and only if $\gcd (a,m)=1$. Moreover, when $\gcd (a,m)=1$, the multiplicative inverse is unique.

Inverses in ${\mathbb{Z}}_p$ (INV ${\mathbb{Z}}_p$)

For all prime numbers $p$ and non-zero elements $[a]$ in ${\mathbb{Z}}_p$, the multiplicative inverse $[a{]}^{-1}$ exists and is unique.