Moment of Inertia

Similarly to the meaning of Mass, you can think of the moment of inertia of an object as its tendency to resist rotation.

Moment of Inertia for a single particle $I_{cm}=M{R}^2$

Moment of Inertia for point-particles $I={\sum }_i{m}_i{r}_i^2$

For continuous distributions of mass, $I={\int }_{body}{r}^{2}dm$

Tip

An object’s moment of inertia really depends on its axis of rotation.

Always the case: $dI=r^{2}dm$ $I=\int dI$ Coordinate System

Common values for Moment of Inertia

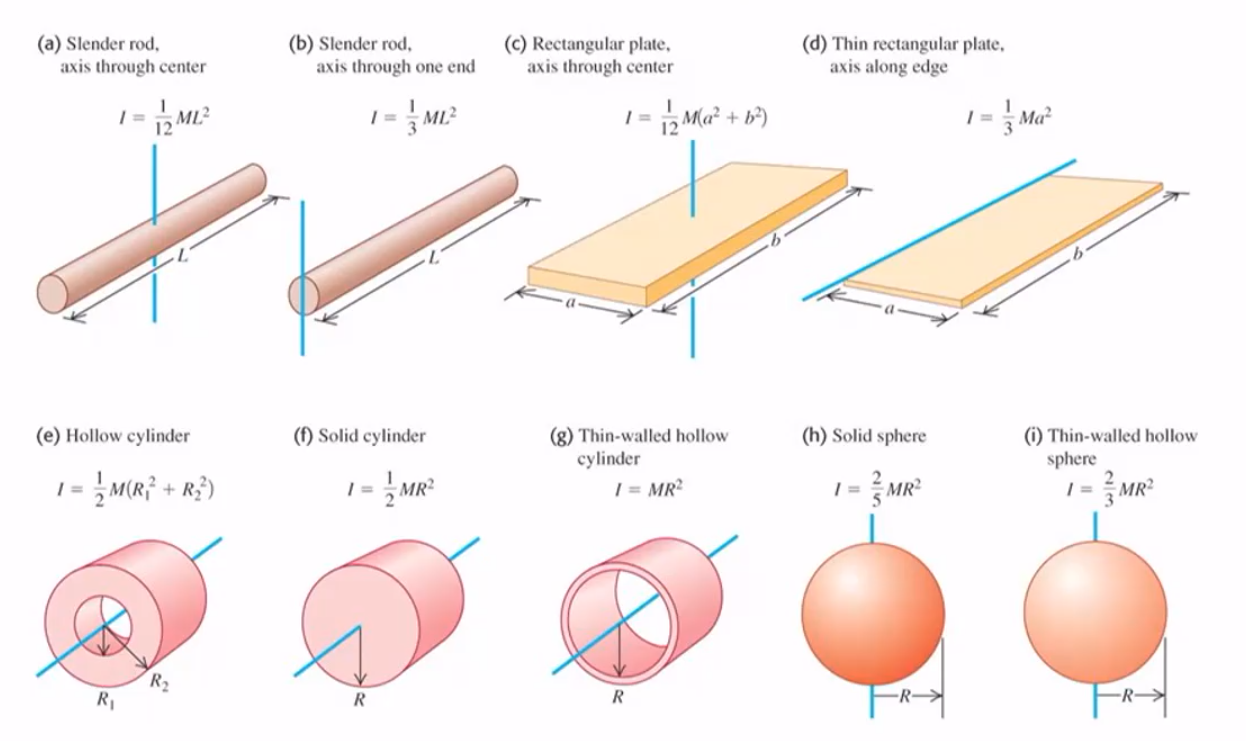The above might be confusing because a hollow shape actually has a higher moment of inertia, although it has less mass.

IMPORTANT YOU NEED TO KNOW HOW TO DERIVE MOMENT OF INERTIA FOR VARIOUS SHAPES #gap-in-knowledge

Problems

Parallel-Axis Theorem

So far we have considered moments of inertia for objects rotating about an axis through the centre of mass of the object. In many applications, the rotation axis does not run through the centre of mass. The calculation of the moment of inertia depends on the axis of rotation, and one needs to find the correct moment of inertia for each situation

$I_a^{object}=I_{cm}^{object}+M{d}^2$ where $d$ is the distance between the object’s center of mass ($cm$) and point $a$.

Rotational Inertia Matrix

A list of the matrices for common shapes is available here. I saw this on the URDF.