Discretization

Had this talk first with Soham about discretizing lines into a discrete space, and I was like, this is hard?

Discretization is really an important problem that I must understand how to solve.

The hard part about discretizing an MDP is figuring out this new transition model.

There are 2 ways to do it, described in CS287 - Advanced Robotics:

1. Nearest neighbour
2. Stochastic Interpolation

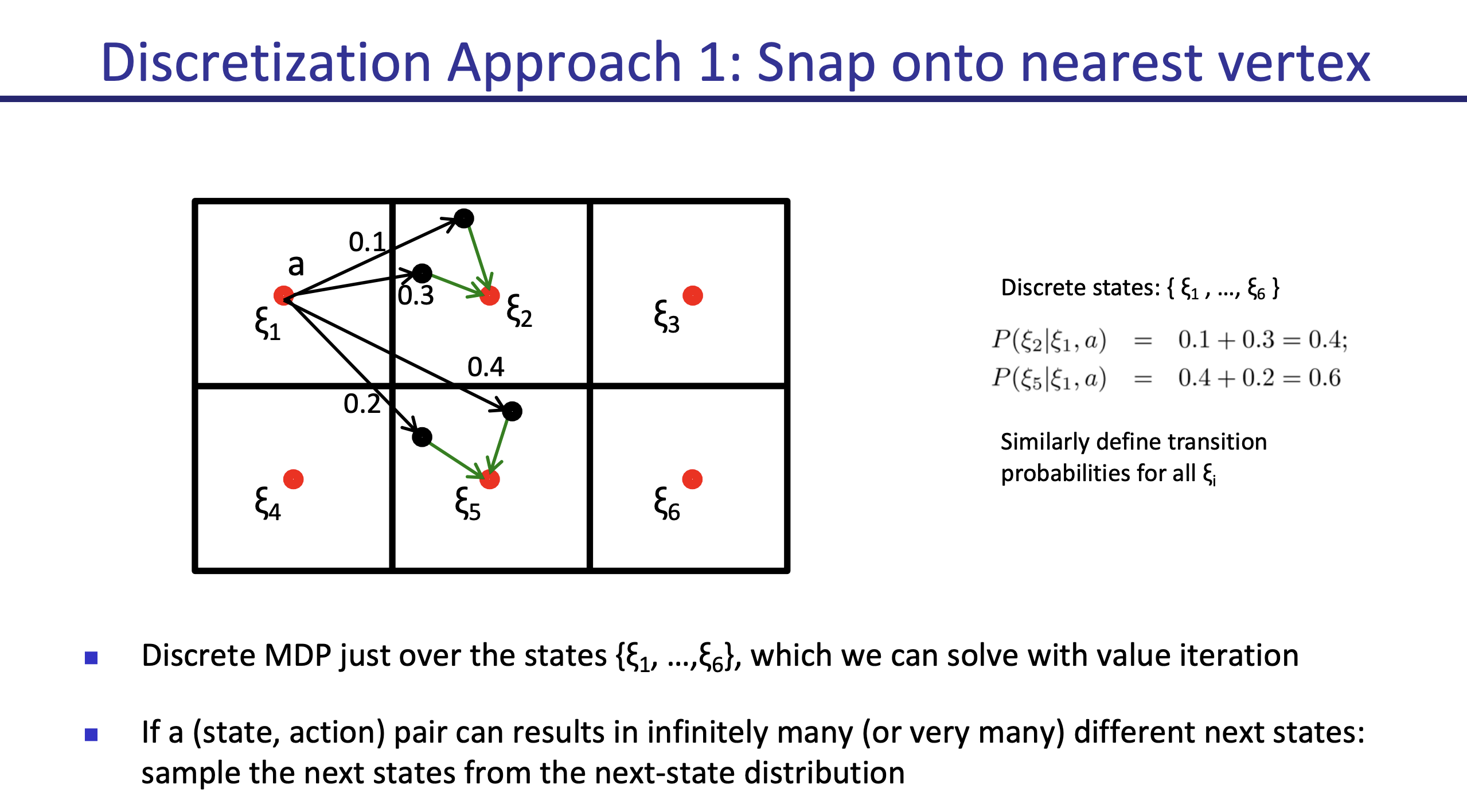
Nearest Neighbour

Find the closest point, snapping to the nearest neighbor (round it off) There are 2 issues:

1. Cheat by moving 0.5 (the bare minimum), and you can snap to the next one
2. It seems like you are not moving, when you really are, just a little bit

Finer and finer grid can help solve these problems.

From an implementation perspective, you define your discrete grid self.state_points. And then find the nearest points to you cont_state by taking the argmin of the absolute difference values.

cont_state = np.expand_dims(cont_state, axis=-1)
if self.mode == 'nn':
	# Get the index of the set of points that is closest to your continuous state
    closest_i = np.argmin(np.abs(self.state_points - cont_state), axis=1)    
	# Get an id from these coordinates (you will use this to index into your transition matrix)
    discrete_state = self.get_id_from_coordinates(closest_i)
    states = np.array([discrete_state])
    probs = np.array([1])

• Note: In the above we assume a transition matrix $T(s,a,s^{\prime })$ of size (S+1, A, S+1), see Value Iteration code as well

Another fastest approach instead to find the closest_i is to use a KD Tree, which finds it in $O(\log n)$ instead of $O(n)$ which is the case for argmin.

• https://stackoverflow.com/questions/10818546/finding-index-of-nearest-point-in-numpy-arrays-of-x-and-y-coordinates

Ahh Serendipity: This was what Soham was doing with the KD Tree.

Stochastic Interpolation

Another solution is to be a little bit more stochastic.

In a 2D grid system,You take the 4 nearest discrete points, and use a transition probability by how close the continuous point is to each of the 4 discrete points.

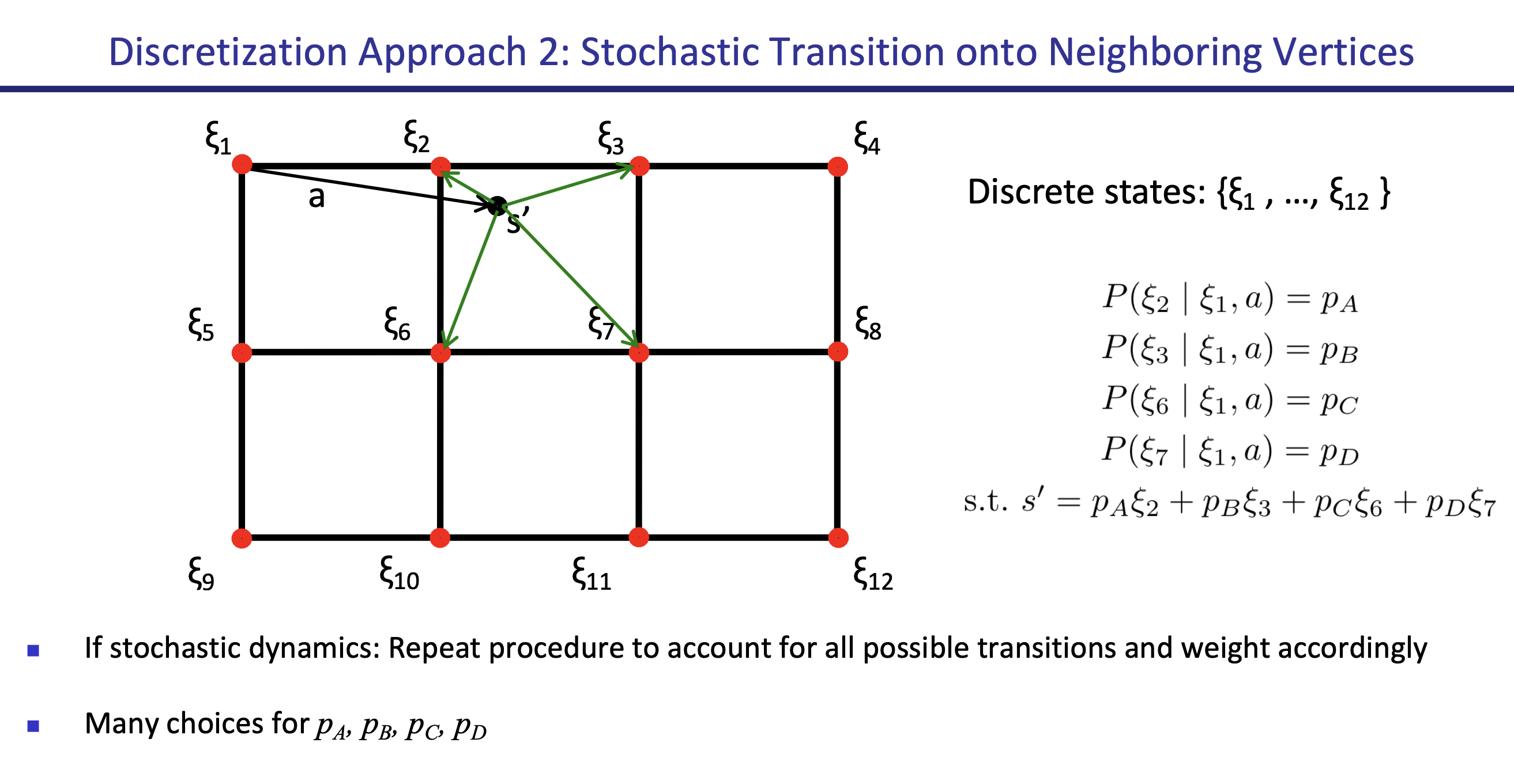
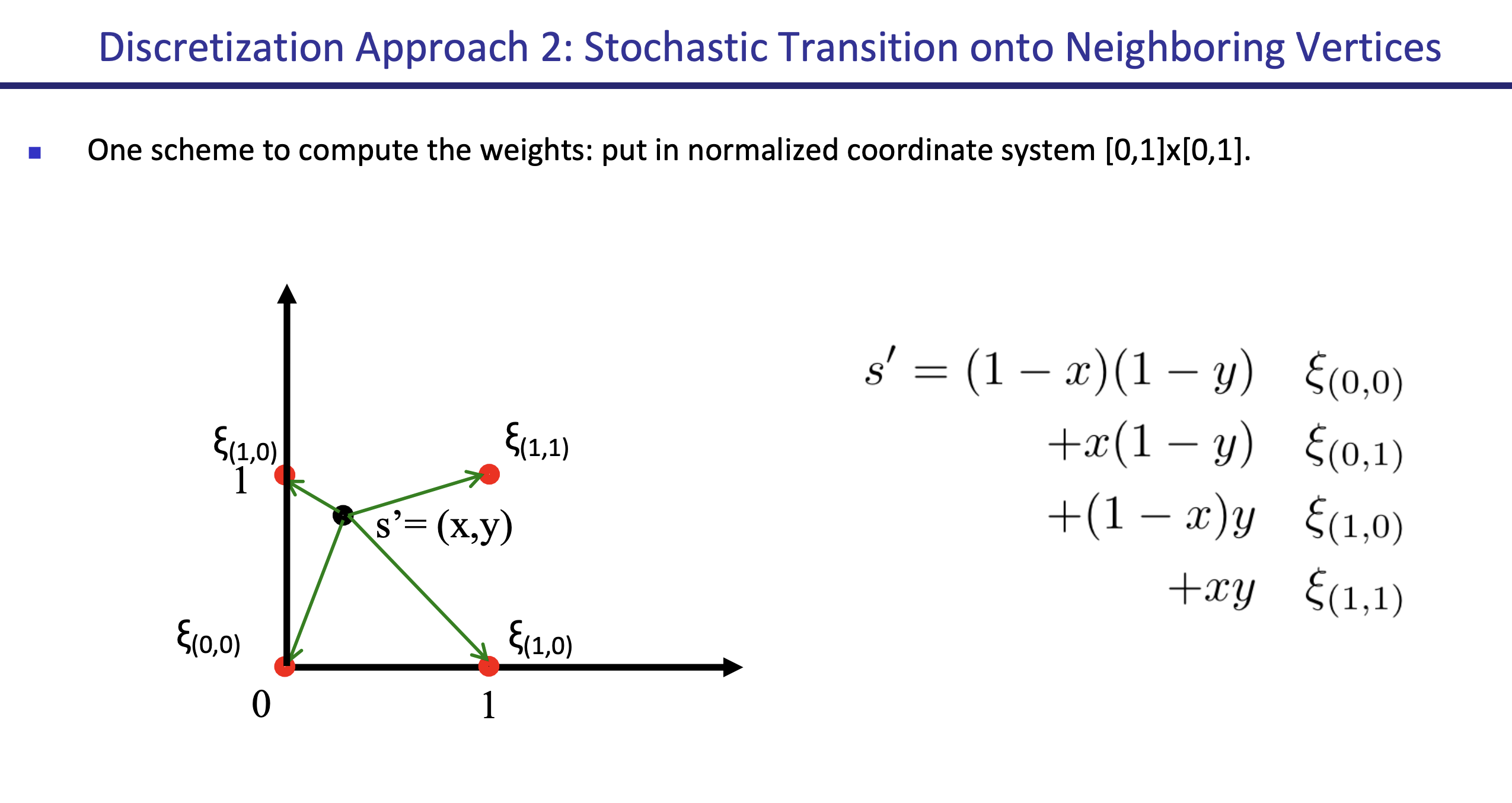
• NOTE: The above is wrong, the $\delta (0,1)$ and $\delta (1,0)$ should switch positions in the diagram.

Implementation

I actually implement discretization in homework 1, which is super cool, because I get hands-on experience now.

Some examples of continuous spaces that I need to solve:

• Mountain Car
• Double Integral

How to Act

Misc