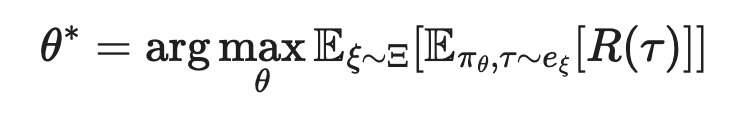Sim2Real

Domain Randomization

I heard this first from Lilian Weng’s video: https://www.youtube.com/watch?v=VTSsFVtVXT4&t=1654s Also introduced in this autonomous drone racing video.

Resources

• You should just consult her article by Lilian Weng
• Domain Randomization for Transferring Deep Neural Networks from Simulation to the Real World (2017)

Domain randomization create a variety of simulated environments with randomized properties and train a model that works across all of them.

• The idea is that this model would be able to adapt to the real-world environment, as the real system is expected to be one sample in that rich distribution of training variations

Using simulated data is ok, but the AI needs to obtain knowledge that generalizes properly.

Before Domain Randomization in RL, it was super hard to get the robot to generalize the policy from the simulation to the real world.

I don’t get the difference with Domain Adaptation though.

Domain adaptation vs. Domain randomization

• domain randomization = modify the training environment to make the model more robust to changes in the testing environment
• domain adaptation = adapt the model to the new environment

So this is actually really simple! We sample uniformly each parameter that can specify the environment.

• In formal terms: Each parameter ${ϵ}_i$ bounded by an interval, ${ϵ}_i\in [{ϵ}_i^{low},{ϵ}_i^{high}]$,$i=1\dots ,N$ is uniformly sampled within the range.

Where does this parameter get fed? Is this something that is captured in the transition function? In the UED, they talk about this.

What are some parameters that we can change?

A model trained on simulated and randomized images is able to transfer to real non-randomized images.

• Position, shape, and color of objects,
• Material texture,
• Lighting condition,
• Random noise added to images,
• Position, orientation, and field of view of the camera in the simulator.

Physical dynamics in the simulator can also be randomized (Peng et al. 2018). Studies have showed that a recurrent policy can adapt to different physical dynamics including the partially observable reality. A set of physical dynamics features include but are not limited to:

• Mass and dimensions of objects,
• Mass and dimensions of robot bodies,
• Damping, kp, friction of the joints,
• Gains for the PID controller (P term),
• Joint limit,
• Action delay,
• Observation noise.

How this looks like

The p. licy is exposed to a variety of environments and learns to generalize. The policy parameter $\theta$ is trained to maximize the expected reward $R(.)$ averaged across a distribution of configurations: