Eigenvalues and Eigenvectors

Never really had the intuition.

Eigenvector (creds to Ayush for intuition)

An eigenvector $v$ of a matrix $A$ is a vector such that multiplication by $A$ alters only the scale of $v$ (a linear transformation).

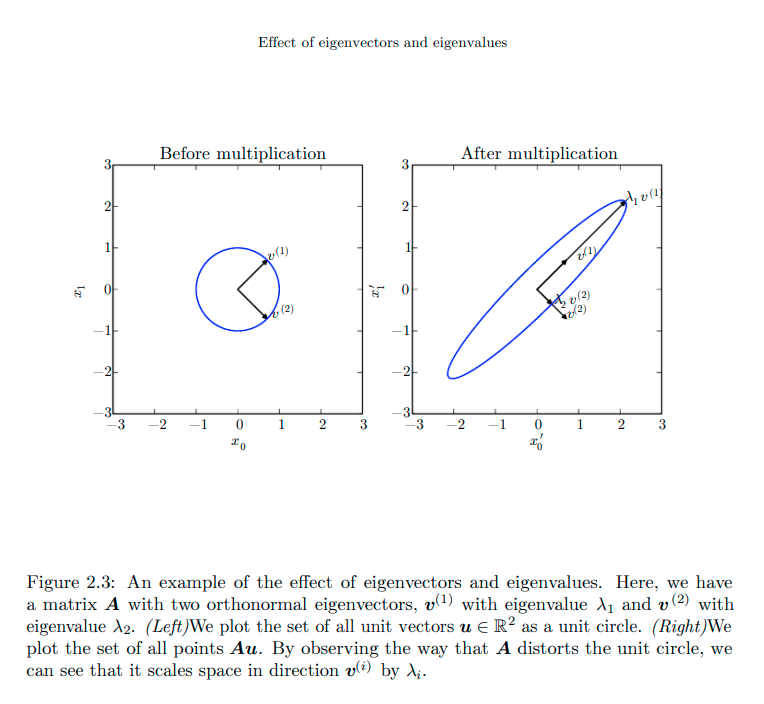
• Source: Deep learning book

Basic Definition

For $A\in M_{n\times n}(\mathbb{R})$, a scalar $\lambda$ is an eigenvalue of $A$ if $A\vec{x}=\lambda \vec{x}$ for some nonzero vector $\vec{x}$. The vector $\vec{x}$ is then called an eigenvector of $A$ corresponding to $\lambda$.

Note

Note that there’s technically an infinite amount of eigenvectors, since you can just vary the scalar multiple and get a different vector. So generally, to uniquely represent an eigenvector, we use the normalized vector.

Determinants and Eigenstuff

$\lambda$ is a eigenvalue of $A$ if and only if satisfies the equation $\det (A-\lambda I)=0$ All nonzero solutions of the homogeneous system of equations $(A-\lambda I)\vec{x}=\vec{0}$ are all of the eigenvectors corresponding to $\lambda$.

Characteristic Polynomial

The characteristic polynomial of $A$ is $C_A(\lambda )=\det (A-\lambda I)$

$\lambda$ is an eigenvalue of A if and only if $C_A(\lambda )=0$.

Non-real eigenvalues

A real matrix can have non-real eigenvalues.

More definitions

Matrix with all positive eigenvalues is called positive definite. Matrix with non-negative eigenvalues is called positive semi-definite. Matrix with all negative eigenvalues is called negative definite. Matrix with non-positive eigenvalues is called negative semi-definite.

Applications

• [[notes/Matrix#Powers of Matrices|Matrix#Powers of Matrices]]

Is this stuff really needed?

For a while, I saw no practical application of this. But it turns out that this kind of stuff is super important in Robotics. For instance, the usage of the Jacobian Matrix for robot control, the eigenvalues of this matrix can be calculated to understand the manipulability of the robot.

• I don’t understand what this means