Feature Point

Harris Corner

Learning from Cyrill Stachniss.

Resources

• Learned from the Visual Feature lecture: https://www.youtube.com/watch?v=nGya59Je4Bs&list=PLgnQpQtFTOGRYjqjdZxTEQPZuFHQa7O7Y&index=14&ab_channel=CyrillStachniss
  • slides here
• Wikipedia also has solid formulas: https://en.wikipedia.org/wiki/Harris_corner_detector
• Slides from CMU https://www.cs.cmu.edu/~16385/s17/Slides/6.2_Harris_Corner_Detector.pdf

Criterion:

$$\begin{array}{rl}R& =\text{Det}(M)-k(\text{Trace}(M){)}^2\\ & ={\lambda }_1{\lambda }_2-k({\lambda }_1+{\lambda }_2{)}^2\end{array}$$

• $M$ is the Structure Matrix
• ${\lambda }_1$ and ${\lambda }_2$ are the two eigenvalues of the structure matrix
• $k\in [0.04,0.06]$

So in practice, we write it as a system of equations and solve for ${\lambda }_1$ and ${\lambda }_2$

$\text{Det}(M)-k(\text{Trace}(M){)}^2={\lambda }_1{\lambda }_2-k({\lambda }_1+{\lambda }_2{)}^2$

Solving the equation

Cyrill Stachniss seems to approach this in a different way? I just reasoned this out, also getting the help of ChatGPT.

The eigenvalues of a matrix $M$ are found by solving the characteristic equation $\text{det}(M-\lambda I)=0$, where $I$ is the identity matrix and $\lambda$ represents the eigenvalues.

For the 2x2 Structure Matrix $M$ of the Harris Corner Detector,

$$M=\left[\begin{array}{cc}{\sum }_{\text{W}}{J}_x^2& {\sum }_{\text{W}}{J}_x{J}_y\\ {\sum }_{\text{W}}{J}_y{J}_x& {\sum }_{\text{W}}{J}_y^2\end{array}\right]$$

Rewriting the matrix in simpler terms $M=\left(\begin{array}{cc}A& C\\ C& B\end{array}\right)$ the Characteristic Equation is: $\text{det}\left(\left(\begin{array}{cc}A-\lambda & C\\ C& B-\lambda \end{array}\right)\right)=(A-\lambda )(B-\lambda )-C^2=0$ Simplifying, we get: ${\lambda }^2-(A+B)\lambda +(AB-C^2)=0$ Solving this equation gives us the solution to the Eigenvalues.

Notice that $\text{det}(M)=AB-C^2,\text{trace}(M)=A+B$

So we can simply the equation to ${\lambda }^2-(\text{trace}(M))\lambda +\text{det}(M)=0$

• Plug the above in the Quadratic Formula and you will find the 2 eigenvalues

Are there always 2 eigenvalues?

No, a 2x2 matrix can have either one or two distinct eigenvalues. If the matrix is diagonalizable, it will typically have two distinct eigenvalues. However, it may have only one eigenvalue if it is a defective matrix.

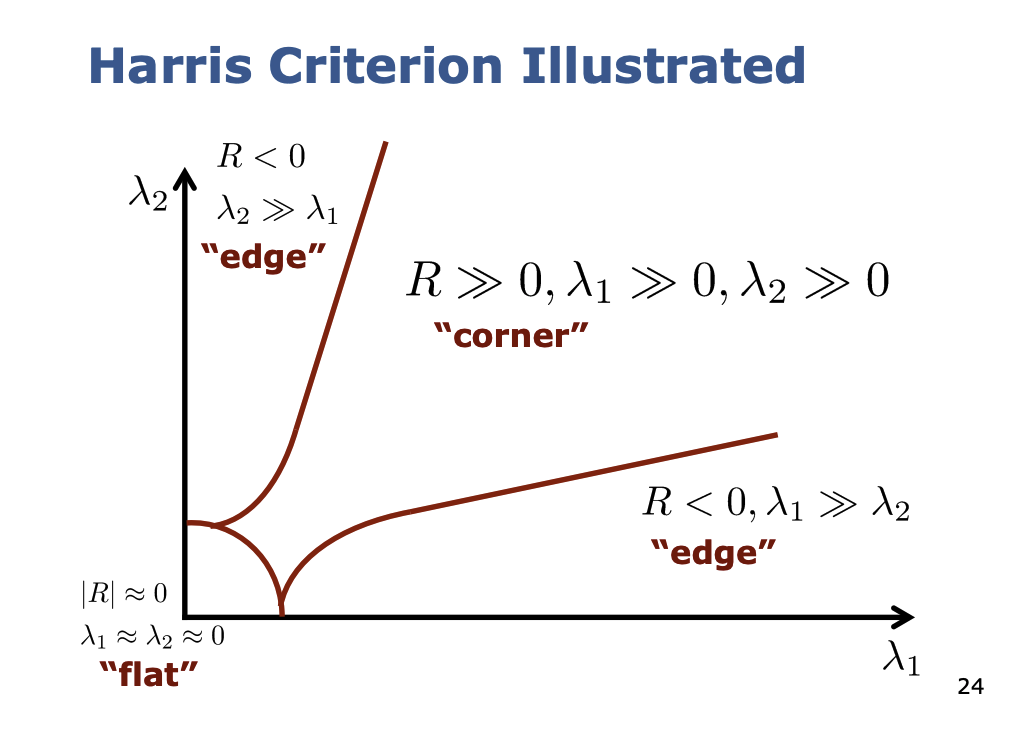
So how is this threshold calculated? I have 2 different eigenvalues, how do I know if ${\lambda }_1>>{\lambda }_2$?

In practice

How fast / slow does this algorithm run?

?

Related

• Shi-Tomasi Corner Detector