Spatial Algebra

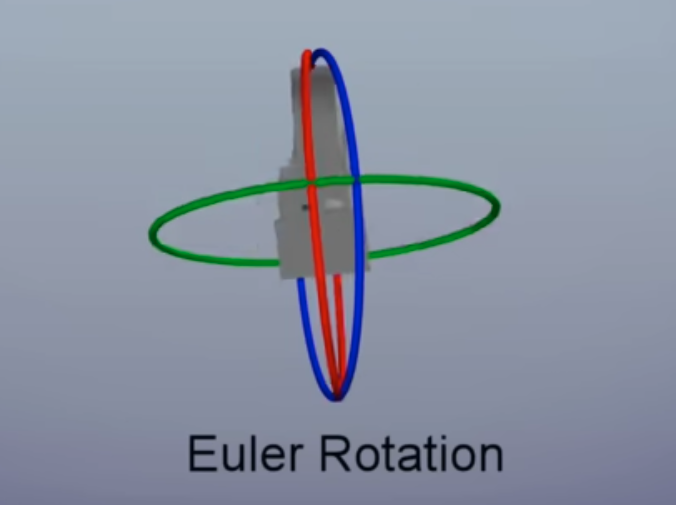
Euler Angle

There are so many issues with Euler Angles. The main reason we use them is that they are very easy to understand for humans. However, they suffer from singularities at angles of $\frac{\pi }{2}$. In these situations, rotations around certain axes become indistinguishable.

I didn’t really understand why they said Right-Hand Rule. You don’t always assume counterclockwise (like in radians). You need to point your thumb in the direction of the axis, and your fingers curl in the positive direction.

Use this tool:

• https://quaternions.online/

Representation of Orientation

In 3D, you can represent an orientation using a sequence of 3 rotations.

Order Matters

Notice that order of rotations matter a LOT. If you pitch by 90 degrees and then roll by 90 degrees, vs. if you roll by 90 degrees then pitch by 90 degrees are going to produce DIFFERENT orientations.

However, even when you fix the order (i.e. specify order of roll-pitch-yaw), there are singularities, i.e. two different sequences produce the same orientation. These singularities happen at angles of $\frac{\pi }{2}$.

Consider $R=R_x(r)R_y(p)R_z(y)$ For a $R=R_x(r)R_y(p)R_z(y)$

• $r$ is roll around the $x$-axis
• $p$ is pitch around the $y$-axis
• $y$ is yaw around the $z$-axis

You can specify a roll, but talking about rotation around x,y and z axis. So imagine we do rpy2r(0.3, pi/2, 0.5). This is equivalent to rpy2r(0, pi/2, 0.8)

This is because Roll and yaw are equivalent at $p=\frac{\pi }{2}$, i.e. $R_x(r)R_y(\frac{\pi }{2})R_z(y)=R_x(r+y)R_y(\frac{\pi }{2})=R_y(\frac{\pi }{2})R_z(r+y)$ And this is why we say we “lose” a degree of freedom, because the yaw can be squashed into the roll, and vice-versa. The physical manifestation of this is Gimbal Lock.

So what is the issue?

It’s really when you try to interpolate where you have also these issues (and consequently derivatives as you mention below). You would expect it to work like

“These singularities become problematic when we start taking derivatives of rotations, for instance when we write the equations of motion. It is now well understood that it requires at least four numbers to properly represent the group of 3D rotations; the unit quaternion is the most common four-element representation.”

• Robot Manipulation course from MIT

When you try to directly interpolation the angles, you might end up drawing weird pattern even though you’ve requested to draw a straight line from one angle to the other.

• https://www.youtube.com/watch?v=zc8b2Jo7mno&ab_channel=GuerrillaCG

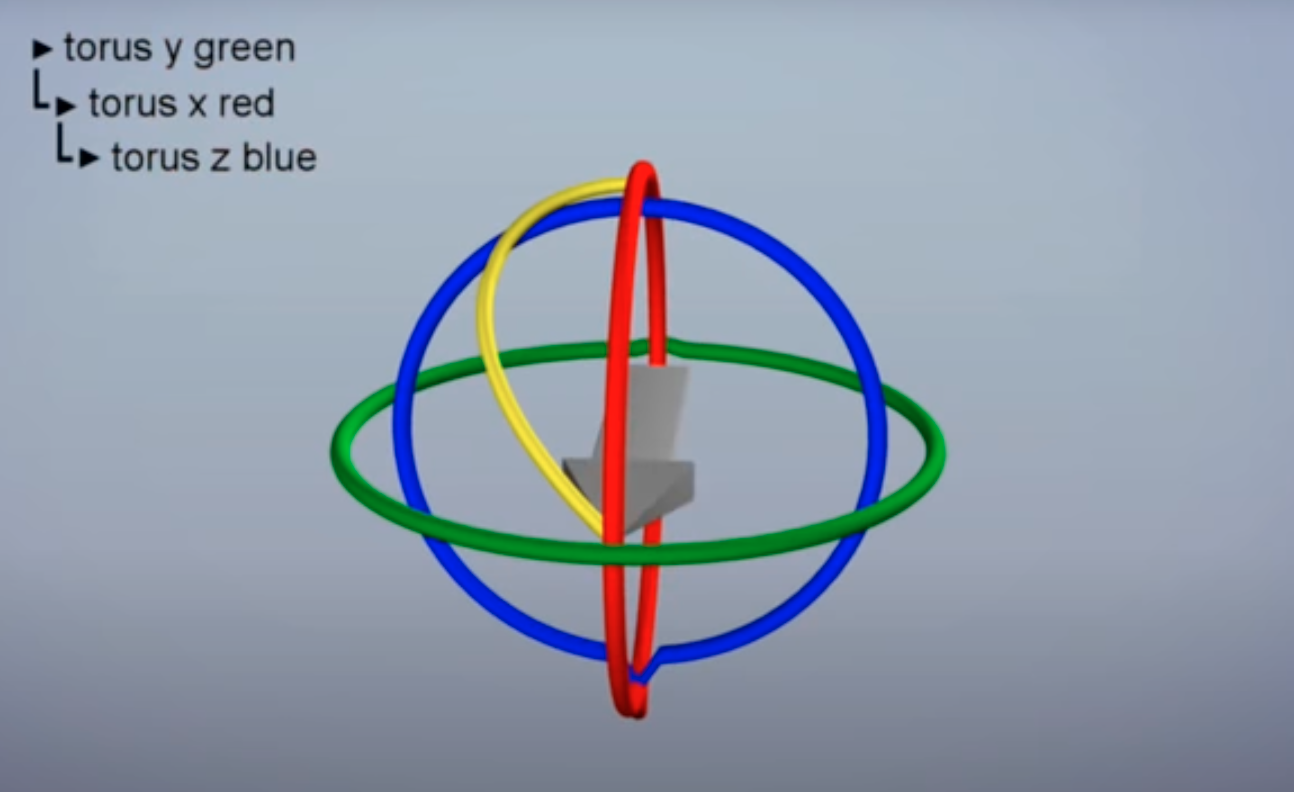
Representation

These Euler angles are represented is using Rotation matrices.

• Note that you can’t just interpolate the rotation matrix, else you just end up with matrices that don’t satisfy the constraint

In Eigen

You usually extract the eulerAngles from the Rotation Matrix, so something like this

Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX order, i.e. roll pitch yaw order

Related

• Quaternion (better representation)

Euler Angles: Do Axes Shift?

with Euler angles, do the axes shift with the order?

• Finally cleared up with the help of Swapnesh.

The axes are fixed as you calculate the Euler rotation.

More Info

In Euler angle rotations, the concept of “intrinsic” versus “extrinsic” rotations becomes important.

• Intrinsic rotations are rotations about the axes of the rotating coordinate system, which changes its orientation after each rotation. This means that the axes do indeed shift with each rotation.
• Extrinsic rotations are rotations about the axes of a fixed coordinate system. In this case, the axes do not shift.

Assume Extrinsic Rotation

That is what Swapnesh told me.

This is

The order of rotations is crucial because rotations are not commutative. In simpler terms, rotating an object 30 degrees about the x-axis and then 40 degrees about the y-axis will not yield the same result as rotating 40 degrees about the y-axis followed by 30 degrees about the x-axis.

This is true?!

ZYX euler angle rotation is equivalent to XYZ fixed axis rotation which is nothing but roll pitch and yaw..

XYZ is equivalent to ZYX fixed axis!

• I need to double check this, and understand why

Actually read the wikipedia page https://en.wikipedia.org/wiki/Euler_angles#Tait.E2.80.93Bryan_angles

Related

• Rotation Matrix
• Axis-Angle Representation
• Quaternion