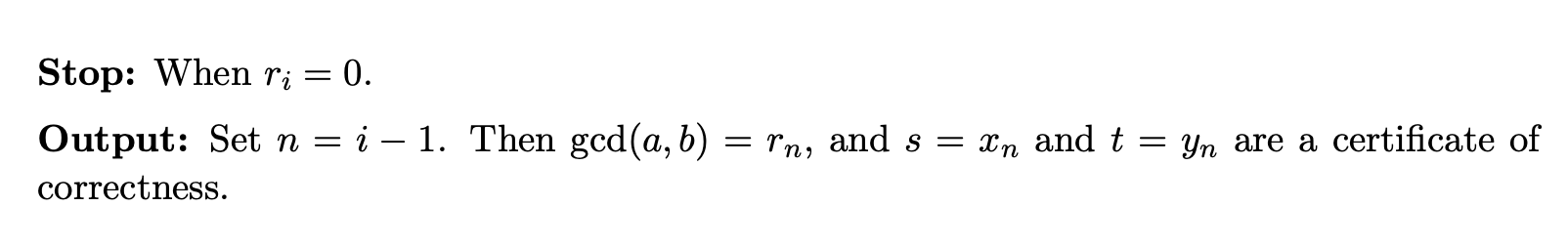Extended Euclidean Algorithm (EEA)

The extended Euclidean Algorithm allows us to calculate $\gcd (a,b)$, and solve the Linear Diophantine Equation for $\gcd (a,b)$ in terms of $a$ and $b$, where $ax+by=\gcd (a,b)$

We know that an answer always exists from Bezout’s Lemma.

LCM and GCD

int gcd(int a, int b) { // Euclidean Algorithm, however this is already implemented in C++
    if (b == 0) return a;
    return gcd(b, a % b);
}
 
int lcm (int a, int b) {
    return a / gcd(a, b) * b;
}

Recursive (implements EEA)

int gcd(int a, int b, int& x, int& y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    int x1, y1;
    int d = gcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - y1 * (a / b);
    return d;
}
 

Iterative (i think the way we learned in class), faster than recursive above

int gcd(int a, int b, int& x, int& y) {
    x = 1, y = 0;
    int x1 = 0, y1 = 1, a1 = a, b1 = b;
    while (b1) {
        int q = a1 / b1;
        tie(x, x1) = make_tuple(x1, x - q * x1);
        tie(y, y1) = make_tuple(y1, y - q * y1);
        tie(a1, b1) = make_tuple(b1, a1 - q * b1);
    }
    return a1;
}
 

There is something very important to observe about the table. If we are computing $\gcd (a,b)$, then for each row of the table we have $a{x}_i+b{y}_i=r_i$

Input: Integers $a$, $b$ with $a\ge b>0$ Initialize: Construct the table with four columns so that

• the columns are labeled $x,y,r\text{and }q$,
• the first row in the table is $(1,0,a,0)$,
• the second row in the table is $(0,1,b,0)$.

Repeat: For $i\ge 3$,

• $q_i\leftarrow \lfloor \frac{r_{i-2}}{r_{i-1}}\rfloor$
• ${\text{Row}}_i\leftarrow {\text{Row}}_{i-2}-q_i{\text{Row}}_{i-1}$

Stop: When $r_i=0$ Output: Set $n=i-1$. Then $\gcd (a,b)=r_n$, and $s=x_n$ and $t=y_n$ are a certificate of correctness.