Memory Model

Flat Memory Model (Linear Memory Layout)

The primary focus of the flat memory model is to enable efficient row-major access to the data.

I first heard about this when asked about it for my Matician interview, but it was concretely explained to me in chapter 3 of PMPP.

In stack allocated arrays, the compilers allow the programmers to use higher-dimensional indexing syntax such as d_Pin[j][i] to access their elements.

Under the hood

However, the compiler actually linearizes this 2D array into an equivalent 1D array and translates the multidimensional indexing syntax into a one-dimensional offset.

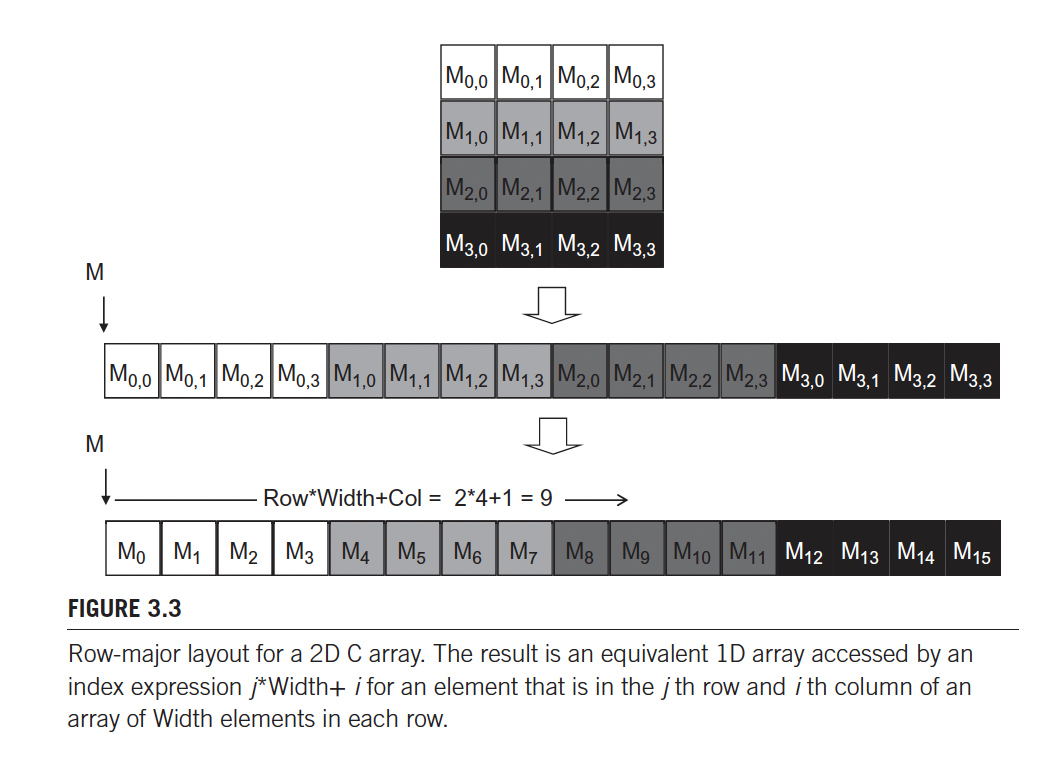
• In dynamically allocated arrays, the work of such translation is up to the programmer.

In C++, you can’t do something like

int** a = new int[100][100];

The work around is doing

int** arr = new int*[100];
for(int i = 0; i < 100; ++i)
    arr[i] = new int[100];

• but this doesn’t guarantee that each element of the array are in contiguous memory blocks

Therefore, it is better to linearize it and prevent cache misses

int* arr = new int[10000];

More Readings

• https://www.geeksforgeeks.org/dynamically-allocate-2d-array-c
• https://learn.microsoft.com/en-us/windows/ai/directml/dml-strides (recommended from Kajanan)

My drawing of a linearized array :) (used in explanation for Matrix Multiplication (Compute)):

CUDA

In CUDA, there the CudaMallocPitch function, that automatically takes care of allocating 2d arrays for you.

In CUDA

Matrices in CUDA are typically stored in row-major order by default, similar to the storage format used in C and C++.