Hashing

Hash functions accept a key and return an output unique only to that specific key.

• This is known as hashing, which is the concept that an input and an output have a one-to-one correspondence to map information.
• Hash functions return a unique address in memory for that data.

A hash function takes a key value and calculates a valid bucket index. We want to use hashing to get constant operation time $O(1)$. However, there might be a Hash Collision.

I finally learned this a little more seriously in CS240.

Formalization in CS240

Define all keys to come from some universe $U$. (Typically U = non-negative integers, sometimes |U| finite.)

• We design a hash function $h:U\to \{0,1,...,M-1\}$. (Commonly used: $h(k)=k\mathrm{mod}M$. We will see other choices later.)
• Store dictionary in hash table, i.e., an array $T$ of size $M$.
• An item with key $k$ should ideally be stored in slot $h(k)$, i.e., at $T[h(k)]$.

Implementing Hashing

There are two main ways to implement hashing:

1. Use Chaining (it’s basically a linked list)
2. Use Open Addressing

1. Open Hashing with Chaining

With open hashing, each bucket holds a pointer to a list rather an element. So it’s basically like a Linked List.

2. Closed Hashing with Open Addressing

Closed hashing uses a hash table with $K$ buckets. Contrary to open hashing, we avoid the links needed for chaining by permitting only one item per slot, but allowing a key $k$ to be in multiple slots.

Typically, with closed hashing, you allocate space for all of the table entries in the table itself at the beginning. As we add more and more data entries, it becomes harder and harder to find an empty slot.

Linear probing means keep adding one to the index ($\mathrm{mod}K$) and check again.

Load factor should be less than 80% to be efficient.

The average bucket-size is $\frac{n}{M}=:\alpha$ ($\alpha$ is called the load factor.)

Important characteristics of Hash Function

1. Deterministic, based on key value
2. Good spread of results over buckets (“uniformity”)
3. Cheap to compute
4. Supports a variable range

Think of an analogy to this image:

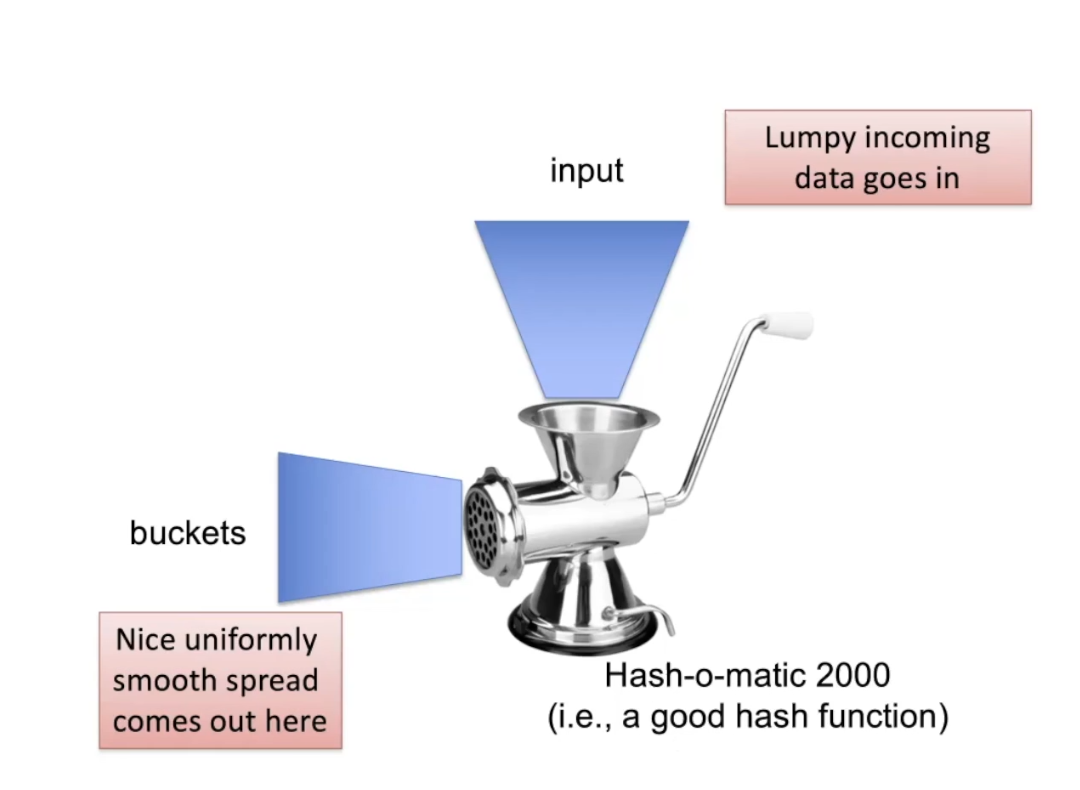
Why isn't a hash function where you simply take the modulus good enough?

Consider the input $10,20,30,40,\dots$ and your hash function is $f(x)=x\mathrm{mod}10$ (hash table of size 10). You run into lots of hash collisions even though your input is uniformly distributed.

Related

• Chaining
• Linear Probing
• Double Hashing
• Cuckoo Hashing
• Hash Collision
• String Hashing
• Merkle Tree
• Locality-Sensitive Hashing