Moment of Inertia

Torque / Moment

Definition: The tendency of a force to cause a rotation about a point or axis is called torque (SI in $Nm$). Note that torque is a vector quantity. This is essential in 3D.

Video

• What is Torque? - Torque basics explained - YouTube by Engineering Mindset

$\vec{\tau }=\vec{r}\times \vec{F}$

Why is torque not measured in Joules?

Work is also measured in $Nm$, which is algebraically the same as Joules. So if you think about it logically, torque should also be in Joules?

We don’t write torque in joules to avoid confusion. Work is the result of a dot product (therefore it is a scalar value). Torque is the result of a cross product (therefore still a vector).

The other way to think about this is that torque is force at a distance. Work is force through a distance. Same unit dimensions, different measurements. Source

In 2D, most of the time we only need to magnitude since we know the direction, therefore the second formula with $\theta$ is more relevant. The torque is given by $|\vec{\tau }|=rF\sin \theta =r_{\perp }F$

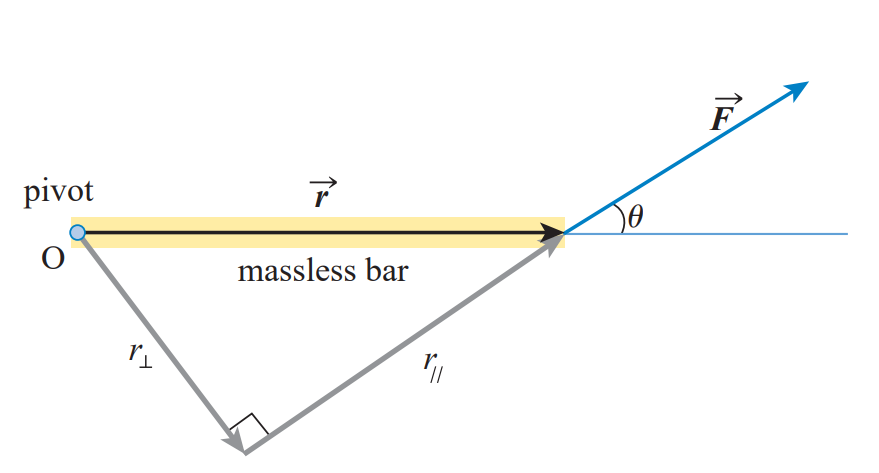The moment arm $r_{\perp }$ (in picture above) is an important notion in engineering. It is is the perpendicular between the point of application of the force and the point.

Torque in terms of angular Acceleration

We can express torque in an analogue form to $F=ma$, Newton’s Second Law in rotation. $\sum \tau =I\alpha$

Worksheet

Varignon’s Theorem (Principle of Moments)

The moment of any force is equal to the algebraic sum of the moments of the components of that force.

If $\vec{F}=\overrightarrow{F_1}+\overrightarrow{F_2}$, then $\vec{r}\times \vec{F}=\vec{r}\times \overrightarrow{F_1}+\vec{r}\times \overrightarrow{F_2}$

Moment of a Force about a Line/Axis#to-review

${\overline{M}}_{line/axis}=[(\overline{r}\times \overline{F})\cdot \hat{u}]\hat{u}$

Moment of a Couple

• Tendency of a pair of forces to cause rotation of a body Forces are:
• Equal in magnitude
• Opposite directions
• Act along parallel LOAs

Couples are a free vector - same rotation effect anywhere in the body

Scalar Method: $|M_B|=|M_A|=|\overline{F}|d_{\perp }$

Vector Method: $M={\overline{r}}_{AB}\times \overline{F}$