Nash Equilibrium
A Nash Equilibrium is a strategy profile in which no players can improve by deviating from their strategies.
Formally, in a two-player extensive game, a Nash Equilibrium is a strategy profile where the two inequalities are satisfied:
- For instance, the first equation states for take any strategy for player in the set of all strategies for player , the expected payoff for player in this strategy profile cannot improve
An approximation of a Nash Equilibrium, called -Nash Equilibrium, is a strategy profile where
Other Way to Think About Nash Equilibrium
When every player is playing with a best response strategy to each of the other player’s strategies, the combination of strategies is called a Nash Equilibrium. No player can expect to improve play by changing strategy alone.
Steps to solve strategic games:
- Set up the game
- Extensive form (i.e. tree diagram)
- Strategic form (i.e. table diagram)
- Define each player’s set of strategies
- Look for strictly dominant strategies
- If every player has a strictly dominant strategy, you’re done!
- Eliminate strictly dominated strategies.
- Find the pure strategy Nash equilibria of the game.
- Find the mixed strategy Nash equilibrium of the game
Two ways to think about Nash Equilibrium:
- At a Nash equilibrium, each player’s strategy is a Best Response to the other players’ strategies.
- A Nash equilibrium is a mutual best response.
The Nash equilibrium is a decision-making theorem within game theory that states a player can achieve the desired outcome by not deviating from their initial strategy. In the Nash equilibrium, each player’s strategy is optimal when considering the decisions of other players.
In two-player Zero-Sum Games, playing a Nash equilibrium ensures you will not lose in expectation.
Exploitability: Distance form a Nash equilibrium Nash Equilibrium exists in any finite game.
There are two types of Strategy Equilibrium:
- Pure strategy equilibrium
- Using Method 1:
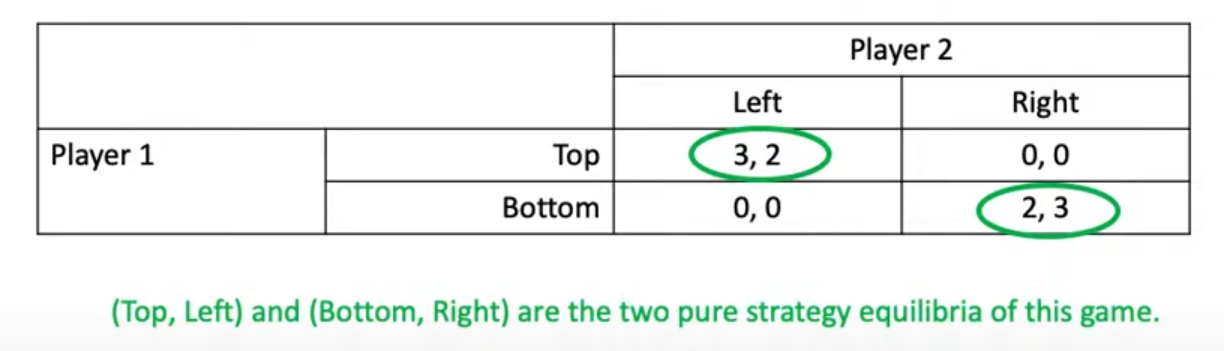 , because no player has an incentive to change their action.
, because no player has an incentive to change their action. - Using Method 2 (Best-Reply):
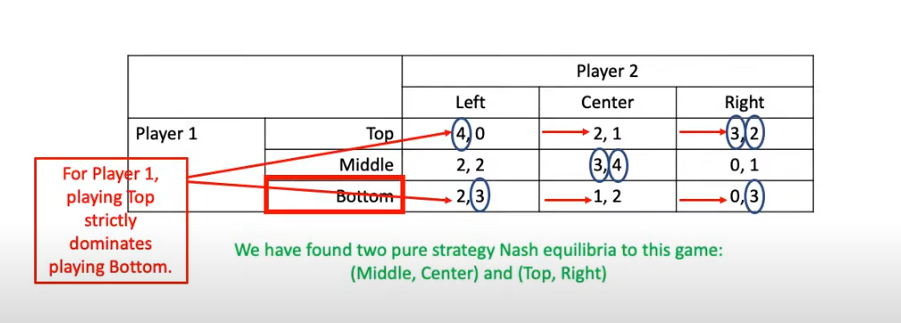
- Using Method 1:
- Mixed strategy equilibrium?
- Assign probability to each strategy for each player
- Calculate the probability of each outcome of the game
Real-world AI must be robust to adversarial adaptation and exploitation.
Some other notes:
- Every game with a finite set of outcomes has at least one equilibrium (However, not guaranteed that this equilibrium is from pure strategy)
- Nash equilibria will not contain strictly dominated strategies.
- Some Nash equilibria might contain weakly dominated strategies.
Exploitability
A best response is a strategy for player that is optimal against .
Exploitability of is defined as where is a Nash equilibrium.
Related
Resources: