Non-Deterministic Finite Automaton (NFA)

It might seem at a surface level that NFAs seem more powerful than DFAs, but they are not.

title: Non-Deterministic Finite Autonomaton
This is pretty much the same as the [[Deterministic Finite Automaton|DFA]], except for $\delta$.
A deterministic finite automaton (DFA) is a five-tuple $\langle h, Σ, Q, q_0, A, \delta_i \rangle$ where: 
- $\sum$ is a finite set of symbols (the alphabet).  
- $Q$ is a finite set of states. 
- $q_0 \in Q$ is the start state. 
- $A \subseteq Q$ is the set of accepting states. 
- $δ : Q \times \sum → \mathbf{2^Q}$ is the transition function that, given a state $q$ and alphabet symbol $a$, returns the new state $q'$ to transition to after processing the symbol $a$ in state $q$ ($2^Q$ is the set of all subsets of $Q$)

$ϵ$-transitions

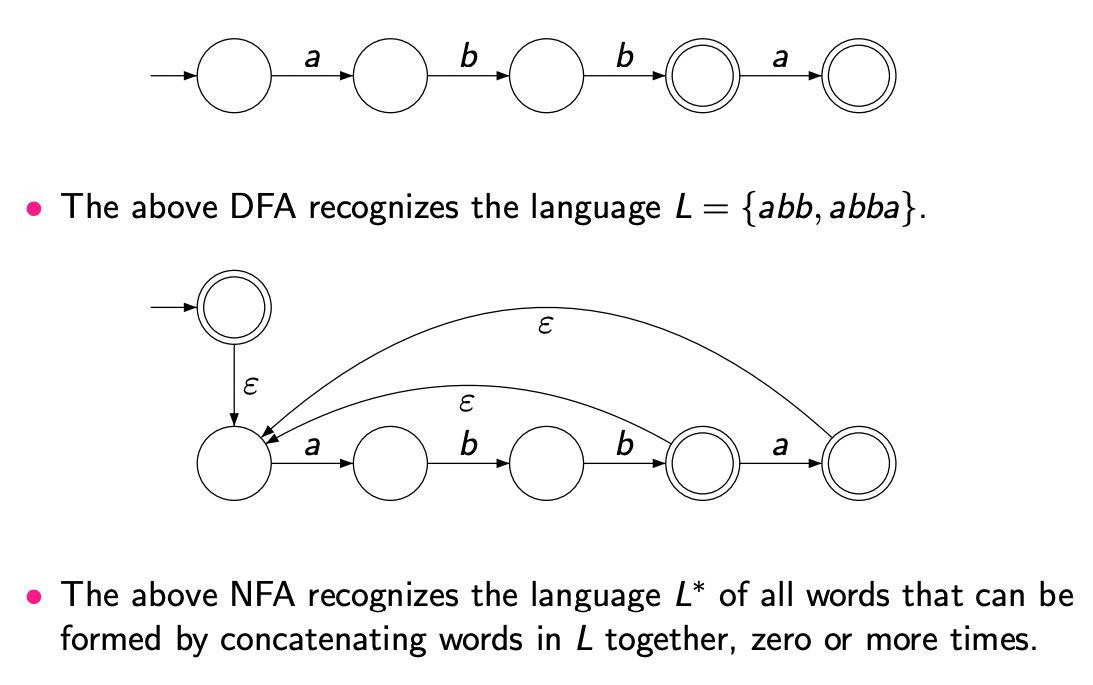
To make it easier to more systematically combine NFAs, we add $ϵ$-transitions. Whenever the NFA is in a state with an outgoing $ϵ$-transition, it may optionally choose to follow that transition without processing any symbols from the input word.

Using $ϵ$-transitions, we can combine the two DFAs without having to modify them, just by adding a new start state with $ϵ$-transitions to the former start states of the two DFAs, as shown in the following diagram:

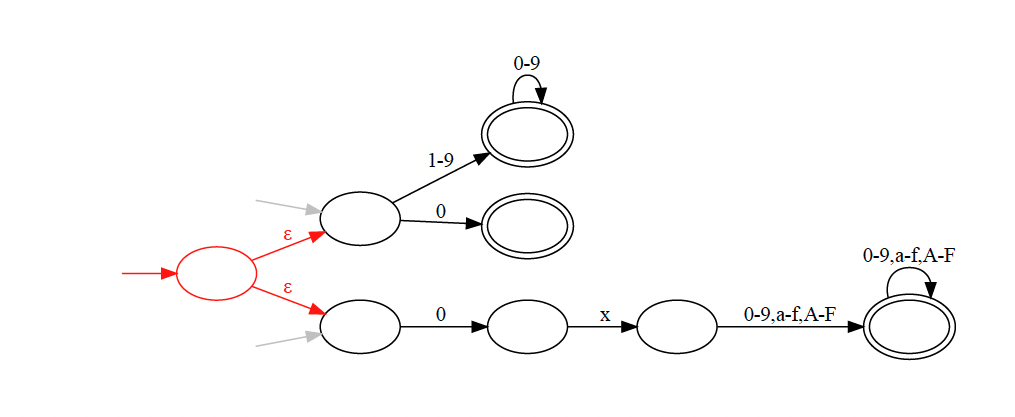
From the new start state, a path through the NFA starts by following one of the $ϵ$-transitions to one of the former start states, depending on whether the input word is a decimal or hexadecimal number.

So the $ϵ$ transition is optional. The example below illustrates this: