Deterministic Finite Automaton (DFA)

A DFA is a directed graph whose nodes are called states and whose edges are called transitions.

In the context of studying Formal Languages in Formal Languages in CS241E, I lerned to use DFAs to do 2 things:

1. Solve the recognition problem: given a word $w$, is $w$ in the specified language $L$? [[notes/Deterministic Finite Automaton#Recognition|Deterministic Finite Automaton#Recognition]]
2. Implement Scanning for a Regular Language

title: Deterministic Finite Autonomaton
A deterministic finite automaton (DFA) is a five-tuple $\langle \sum, Q, q_0, A, \delta \rangle$ where: 
- $\sum$ is a finite set of symbols (the alphabet)
- $Q$ is a finite set of states
- $q_0 \in Q$ is the start state
- $A \subseteq Q$ is the set of accepting/final states
- $δ : Q \times \sum → Q$ is the transition function that, given a state $q$ and alphabet symbol $a$, returns the new state $q'$ to transition to after processing the symbol $a$ in state $q$

In a given state and for a given symbol, there can be at most **one** transition that originates from the state and is labelled with that symbol (multiple transitions NOT allowed). This is because $\delta$ is a [[Function]]! 

Personal Note*: I feel like the above is really similar to the notation I have seen for a Markov Decision Process.

We can define the extended transition function ${\delta }^{\ast }:Q\times {\sum }^{\ast }\to Q,w$ which maps a state $q$ and a sequence of symbols $w$ to a new state $q_0$ as follows: ${\delta }^{\ast }(q,\epsilon )=q(ϵ=\text{empty word})$ ${\delta }^{\ast }(q,first::rest)={\delta }^{\ast }(\delta (q,first),rest)$

title: How to compare two DFAs?
In CS462, there is this theorem that there is a unique smallest DFA (called minimum DFA), so two check that two DFAs are the same, we reduce them to as small as possible and check that they are the same.

The following diagram shows an example of a DFA over the alphabet $\sum =\{a,b\}$ that specifies the language of words that contain an odd number of $a$’s (and any number of $b$’s’):

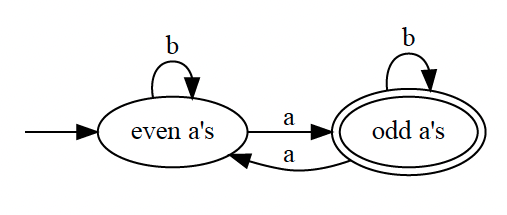
• The double circles means an accepting state

If there is no transition labelled with the symbol, the DFA is said to get stuck and the word is not in the language.

• Serendipity, this reminds me of ideas for Serendipity, this reminds me of ideas for Backup Diagrams??

We can make transitions through the DFA on a sequence of symbols rather than only a single symbol at a time, we say that the DFA accepts a word $w$ if   ${\delta }^{\ast }(q_0,w)\in A$.

Example of a DFA for detecting if an input string is not divisible by 3. This is actually a really clever idea that Chester Chung gave me

lazy val notDiv3 = DFA(  
  alphabet = "01".toSet,  
  states = Set("start", "0mod3", "1mod3", "2mod3"),  
  start = "start",  
  accepting = Set("1mod3", "2mod3"),  
  transition = {  
    case("start", '1') => "1mod3"  
    case("0mod3", '0') => "0mod3"  
    case("0mod3", '1') => "1mod3"  
    case("1mod3", '0') => "2mod3"  
    case("1mod3", '1') => "0mod3"  
    case("2mod3", '0') => "1mod3"  
    case("2mod3", '1') => "2mod3"  
  }  
)

Recognition

Recognition is the process of determining if we are given a word $w$, is it in the specified language $L$?

Below is the implementation of the recognize algorithm:

def recognize(dfa: DFA, input: List[Char]): Boolean = {  
  var i = 0  
  var state = dfa.start  
  var error = false  
  while (i < input.length) {  
    if (dfa.transition.isDefinedAt((state, input(i)))) {  
      state = dfa.transition((state, input(i)))  
    } else {  
      error = true  
    }  
    i += 1  
  }  
  if (error) {  
    false  
  } else {  
    dfa.accepting(state)  
  }  
}

Related

• Kleene’s Theorem
• Non-Deterministic Finite Automaton
• Scanning