Value Function

Optimal Value Function

• The optimal value function specifies the best possible performance in the MDP.
• An MDP is “solved” when we know the optimal value function

Definition

The optimal state-value function $v_{\ast }(s)$ is the maximum value function over all policies for all $s\in \mathcal{S}$ $v_{\ast }(s)=\underset{\pi }{\max }{v}_{\pi }(s)$

The optimal action-value function $q_{\ast }(s,a)$ is the maximum action-value function over all policies $q_{\ast }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)$

It is very similar to the original Value Function, but rather than taking the expected values given some policy, we simply take the maximum of the values over our choices.

Backup Diagrams for 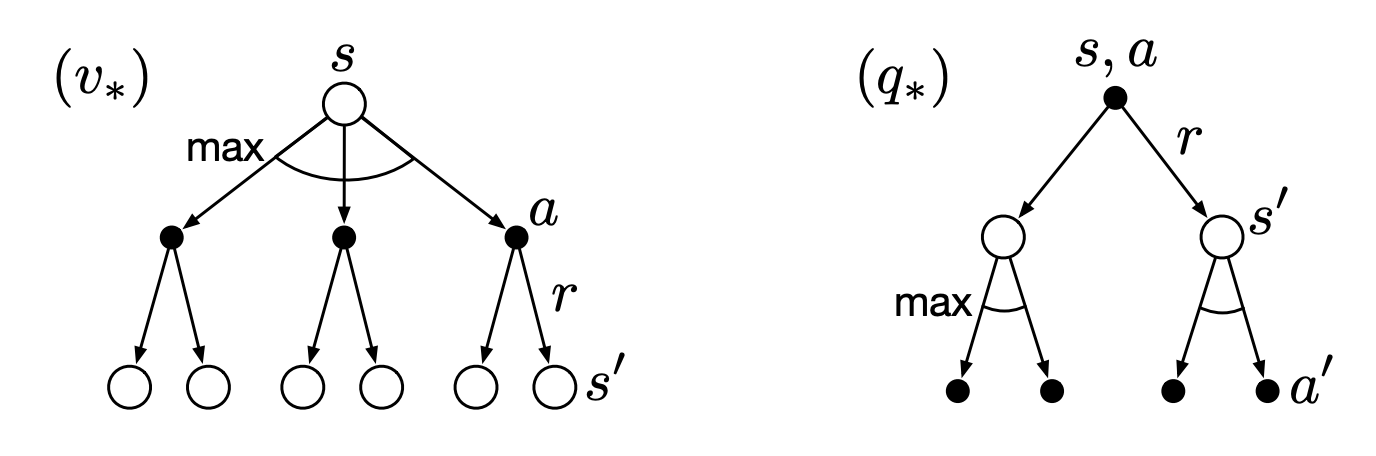$q_{\ast }$ and $v_{\ast }$ Optimal State-Value Function $v_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$ $v_{\ast }(s)=\underset{a}{\max }{\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+\gamma v_{\ast }(s^{\prime }))$

Optimal Action-Value function IMPORTANT: We are taking the average for $q_{\ast }(s,a)$ and not the max, because we cannot control what the environment does to us $q_{\ast }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+\gamma v_{\ast }(s^{\prime }))$ $q_{\ast }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+\gamma \underset{a}{\max }{q}_{\ast }(s^{\prime },a^{\prime }))$

Closely related to Optimal Policy. They are solved using Optimal Policy. They are solved using Bellman Equation.