Value Function, Bootstrapping

Bellman Equation

The bellman equation relates the value of a current state with the value of successive states.

This is the fundamental idea: $\text{Value}=\text{immediate reward}+\text{discounted sum of future rewards (future value)}$ $V^{\pi }(s)={\mathbb{E}}_{\pi }[r+\gamma V^{\pi }(s^{\prime })]$ All of value-learning based RL bases off the above equation.

Bellman Expectation and Bellman Optimality

We have bellman expectation (used in Policy Evaluation) which defines the expected value of a state relating to successor states.

$$\begin{array}{rl}{V}^{\pi }(s)& ={\mathbb{E}}_{a\sim \pi (\cdot |s),s^{\prime },r\sim p(\cdot |s,a)}[r+\gamma V^{\pi }(s^{\prime })]\\ & =\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V^{\pi }(s^{\prime })]\end{array}$$ $$\begin{array}{rl}{Q}^{\pi }(s,a)& ={\mathbb{E}}_{s^{\prime },r\sim p(\cdot |s,a)}[r+\gamma {\mathbb{E}}_{a^{\prime }\sim \pi (\cdot |s^{\prime })}Q(s^{\prime },a^{\prime })]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })]\end{array}$$

We have bellman optimality (used in Policy Improvement), which defines how the optimal value of a state is related to the optimal value of successor states.

$$\begin{array}{rl}{V}^{\ast }(s)& =\underset{a}{\max }{\mathbb{E}}_{s^{\prime },r\sim P}[r+\gamma V^{\ast }(s^{\prime })]\\ V^{\ast }(s)& =\underset{a^{\prime }}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\lambda V^{\ast }(s^{\prime })]\end{array}$$ $$\begin{array}{rl}{Q}^{\ast }(s,a)& ={\mathbb{E}}_{s^{\prime },r\sim p(\cdot |s,a)}[r+\gamma \underset{a^{\prime }}{\max }{Q}^{\ast }(s^{\prime },a^{\prime })]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{\max }{Q}_{\ast }(s^{\prime },a^{\prime })]\end{array}$$

IMPORTANT

Make sure to understand the difference between the bellman expectation backup and bellman optimality backup. This is fundamental in RL:

• The bellman expectation to get the expected values of a particular policy $\pi$
• The bellman optimality to get the optimal value function (these values are obtained if we can somehow find an optimal policy $\pi$)

Visualizing the Bellman Update

These are taken from the RL textbook, and use lowercase $v_{\pi }$ and $q_{\pi }$ as opposed to $V^{\pi }$ and $Q^{\pi }$, but they refer to the same thing.

With the value function, the probability (weight of each edge) is given by the policy, we decide that. Below are called Backup Diagram: 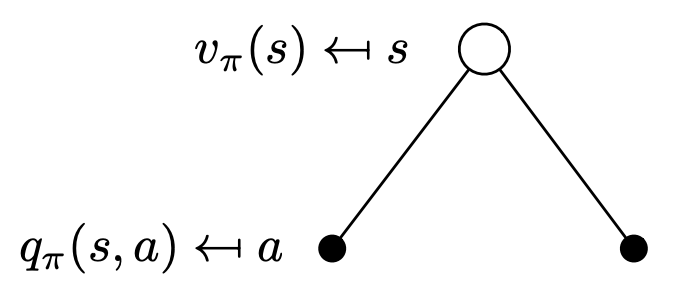$v_{\pi }(s)={\sum }_a\pi (a|s)q_{\pi }(s,a)$ On the other hand, for the q-value (i.e. after we have done an action), this is what we do with the environment. After choosing an action, we get a reward, and the probability of landing into new states are given by our environment. We also apply the Discount Factor here. 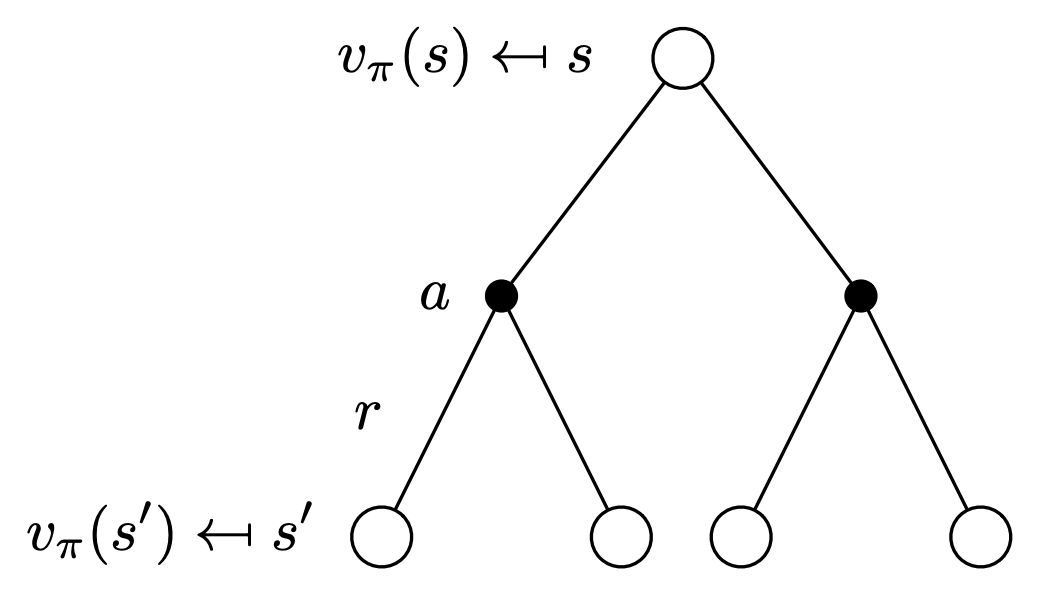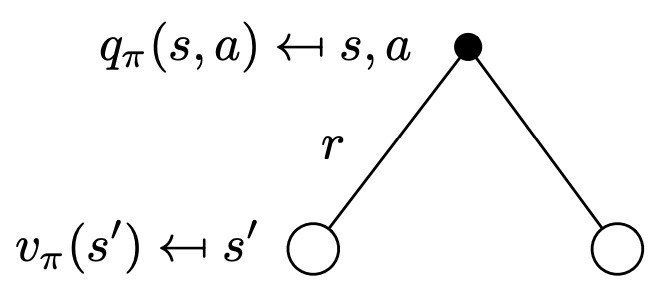$q_{\pi }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+\gamma v_{\pi }(s^{\prime }))$ So now, we can have a recursive relationship. $v_{\pi }(s)={\sum }_a\pi (a|s){\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+\gamma v_{\pi }(s^{\prime }))$ $q_{\pi }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)(r+\gamma {\sum }_{a^{\prime }}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime }))$

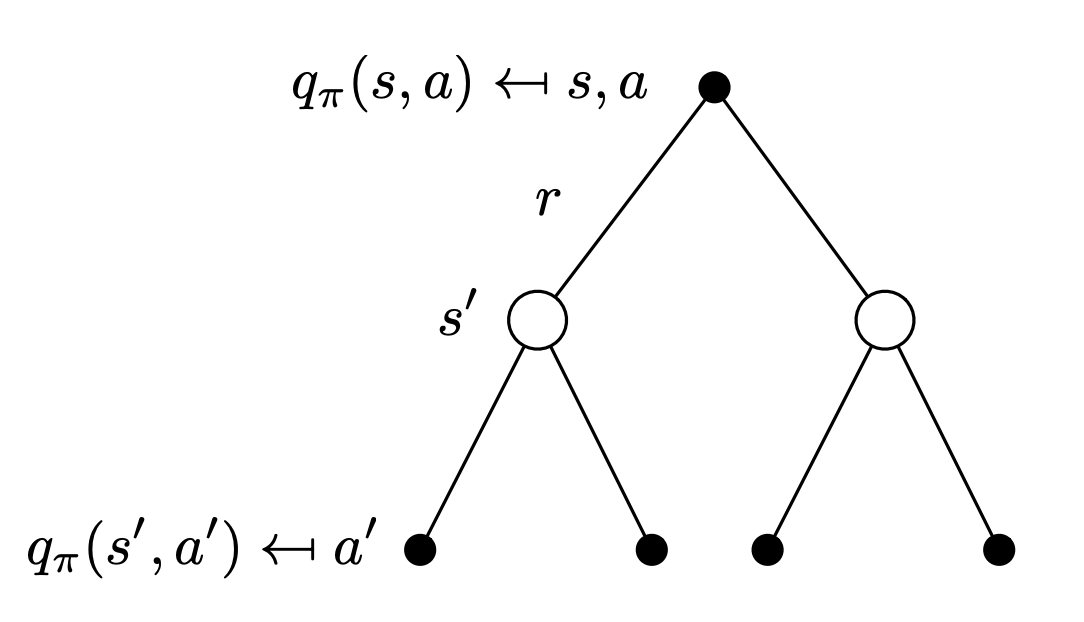
#gap-in-knowledge review david silver lectures, I don’t understand the big picture, why does a 1-step lookahead give you the optimal policy? Page 86 of RL book

• Because of GLIE, the backup structure and GLIE together ensure convergence to optimality

A greedy policy is actually optimal in the long-term sense in which we are interested because $v_{\ast }$ already takes into account the reward consequences of all possible future behavior.

By means of $v_{\ast }$, the optimal expected long-term return is turned into a quantity that is locally and immediately available for each state. Hence, a one-step-ahead search yields the long-term optimal actions.

Solving the Bellman Optimality Equation

Bellman Optimality Equation is non-linear. There are No closed form solution.

Instead, there are many iterative solution methods:

• Policy Iteration
• Value Iteration
• Q-Learning
• Sarsa

Related

• n-step Reinforcement Learning
• Principle of Optimality